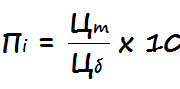Что такое дюрация облигаций и зачем она нужна? просто о сложном

Формула для расчета

,где

i-й Платеж – очередной регулярный платеж, как купон, так и частичное или полное погашение.

Ставка – то, что мы решили принимать за текущую ставку вложений, это может быть или ключевая ставка ЦБ, или средняя ставка на рынке облигаций, или уровень инфляции.

ti – очередной временной период, например 5-й год от начала вложений. Может быть и таким 2,25 – два с четвертью года, если выплаты раз в квартал.

В результате получаем значение Д. в годах.

Иногда формулу расчета упрощают:

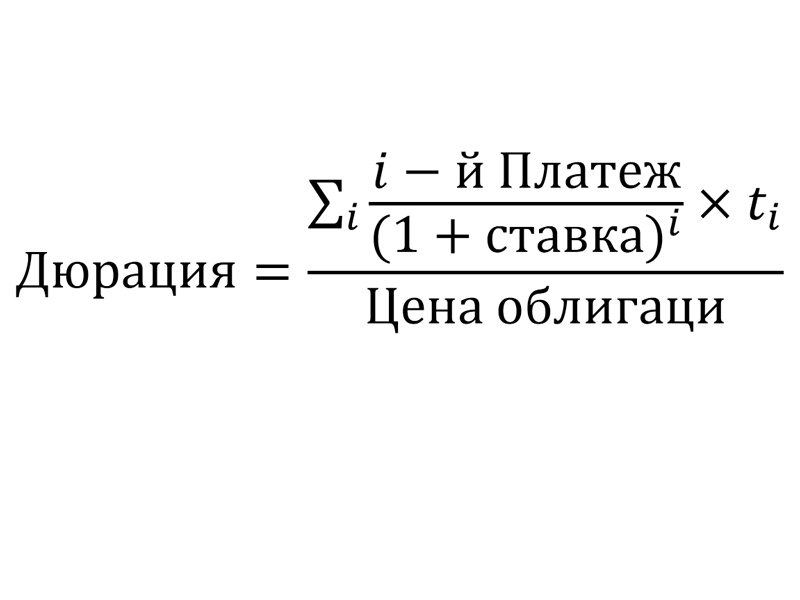
Здесь в знаменателе стоит просто текущая рыночная цена, т.к. предполагается, что она идеально оценивает сегодняшнюю стоимость всех будущих денежных потоков от вложений.

Формула расчета

Существуют два варианта расчета дюрации облигаций: метод Маколея и модифицированный метод. О каждом способе я расскажу отдельно.

Дюрация Маколея

Если говорить о методе Маколея, то в своей формуле он учитывает величину купонного дохода, номинал, альтернативную доходность (усредненный показатель рыночной доходности) и срок, оставшийся до погашения долговой бумаги. Если по бонду не выплачиваются купоны в период обращения, а возврат стоимости и процентов происходит только в момент погашения, то его дюрация по формуле Маколея будет равна сроку до погашения.

Модифицированная дюрация

Модифицированный способ расчета позволяет учесть риск изменения рыночной доходности. Стоимость долговых инструментов меняется в зависимости от рыночных ставок, и инвесторы хотят понять, как сильно изменится цена облигации при смене рыночной доходности.

Формула такого метода выглядит так: MD = D/(1+YTM); где D – Дюрация по методу Маколея, а YTM – доходность к погашению. Например, если взять трехлетнюю бумагу со ставкой в 10 %, доходность к погашению которой будет 9 %, то по методу Маколея показатель будет равен 975 дням. При таких же условиях модифицированный способ расчета покажет результат в 895 дней.

Эффективная

Эффективной называется дюрация, которая учитывает колебания как в сторону увеличения, так и падения. Формула включает в себя разницу между ценой при уменьшении и увеличении ставок, разделенную на начальную стоимость. Если же нет определенного мнения по поводу динамики уровня процентных ставок в будущие периоды, то при формировании облигационного портфеля стоит выбирать бумаги с показателями дюрации, близкими к срокам вашего предполагаемого инвестирования.

Что такое дюрация (ДО) простыми словами

ДО — это длительность возврата капитала, вложенного инвестором в приобретение ценной бумаги.

Формула ДО и что она означает

Показатель вычисляется так:

Эта формула сложна, и инвесторы не пользуются ею. Для конкретного выпуска ДО рассчитывается автоматически в торговом терминале. Главное — понимать, что эта формула означает.

1. Вкладчик рискует меньше, приобретая облигации с меньшей дюрацией.
2. Чем выше ДО, тем сильнее зависит цена купона от политики Центробанка.
3. ДО прямо пропорциональна периоду погашения и обратно пропорциональна доходности.

Модифицированная дюрация (МД)

МД показывает зависимость цены бонда от величины его доходности. Её формула такова:

DM = D / (1+rp),

• где DM – модифицированная;
• D – обыкновенная дюрация;
• rp – доходность.

В реальной жизни DM применяется для установления взаимосвязи между процентными ставками и стоимостью облигаций. Этот процесс имеет вид:

ΔP = (-1) х DM х Δr,

• где ΔP – изменение цены облигации;
• Δr – изменение процентных ставок.

Если ΔP принимает отрицательное значение, это показывает, что при росте ставок ЦБ ценная бумага дешевеет, и наоборот.

Примеры применения на практике

Теперь пришло время поговорить о том, для чего же всё-таки нужно знать такой параметр как ДО, и как его можно применять на практике.

Снижение риска инвестиций

Во-первых, как уже упоминалось выше, дюрация может служить мерой рискованности ваших инвестиций. Чем меньше величина дюрации (читай – срок окупаемости), тем меньше и риск потерять вложенные средства (или часть из них).

Для иллюстрации этого момента давайте рассмотрим простой пример. Представьте себе, что к вам пришли два человека, каждый с просьбой одолжить ему сумму в 1000000 рублей на срок в один год. Каждый из них готов уплачивать проценты в размере 15% годовых, но первый заёмщик готов платить проценты ежемесячно (а размере 15%/12 месяцев = 1,25%), а второй только по истечении года. Кому из них, при прочих равных условиях, вы предпочтёте одолжить деньги?

Ответ очевиден, наиболее выгодным для вас вариантом является одолжить деньги первому заёмщику, который согласен платить проценты ежемесячно. Этот вариант обладает тем неоспоримым преимуществом, что вы начинаете получать возврат инвестированных средств с первого же месяца. А это в свою очередь снижает риск инвестиций (ведь при одинаково неблагоприятном стечении обстоятельств, с первого заёмщика вы получите хоть что-то, в то время как со второго рискуете не получить вообще ничего).

Теперь перейдём к облигациям. Предположим, вы выбираете между двумя облигациями с одинаковыми сроками погашения и стоимостью. Но первая из этих облигаций предполагает выплату купонного дохода раз в месяц, а вторая только раз в год. Соответственно, ДО для первой облигации будет меньше, чем для второй (мы ведь помним, что ДО тем меньше, чем чаще выплачивается купонный доход по ней). И, следовательно, риск инвестиций в первые облигации будет меньшим, чем риск инвестиций во вторые облигации.

Зависимость ДО от процентной ставки

Облигации в целом являются довольно консервативным финансовым инструментом, то есть риск по ним и так минимален (он практически сопоставим с рисками по банковским депозитам). Поэтому дюрацию облигаций чаще рассматривают не в контексте снижения риска, а в контексте зависимости от процентных ставок.

Чтобы проиллюстрировать эту зависимость, давайте рассмотрим простой пример. Предположим, что вы приобрели, на одинаковые суммы денег, два вида облигаций одного и того же эмитента, но с разными сроками погашения. У первых срок погашения через год (ДО меньше), у вторых срок погашения через 10 лет (следовательно, ДО гораздо больше). Купонный доход по обоим видам облигаций составляет 10% годовых.

Теперь предположим, что процентные ставки в стране начали сильно расти и если сегодня выпускали облигации доходностью в 10%, то через некоторое время появляются новые облигации дающие доходность в 12%, а затем и в 15% и в 20%. Как вы думаете, при этом изменится стоимость ваших облигаций дающих 10% годового дохода? Правильно, их стоимость упадет, поскольку спрос на них значительно снизится (зачем людям покупать ваши «десятипроцентные» облигации по прежней цене, если они могут вложить деньги в более доходные бумаги).

Причём стоимость облигаций с большим значением ДО (у которых срок погашения через 10 лет) снизится гораздо больше, чем стоимость облигаций с меньшим значением дюрации (у которых срок погашения через год).

Представим теперь, что события стали развиваться диаметрально противоположным образом и процентные ставки в стране начали падать. То есть если сегодня вложить деньги под 10% годовых можно было относительно легко, то через некоторое время процентная ставка снизится до 5% и вложить деньги под те же 10% (с сохранением того же уровня риска) уже будет попросту невозможно. Очевидно, что при этом варианте развития событий, ваши облигации значительно вырастут в цене, ведь каждый предпочтёт вложить свои деньги под более высокий процент.

Причём, опять же, наиболее вырастут в цене именно облигации с большим значением дюрации (со сроком погашения через 10 лет).

Дюрация облигации: расчет, формула

Величина дюрации может быть использована для характеристики многих инвестиционных инструментов, но чаще всего ее применяют для учета рисков при использовании ценных бумаг с установленным сроком обращения.

Наиболее распространенным использованием показателя дюрации является расчет дюрации облигации. Как уже было приведено выше, дюрация облигации идентична общему понятию дюрации, что представляет собой определенное количество лет, необходимое на погашение полной стоимости облигации.

Облигация является эмиссионной долговой ценной бумагой и ее рыночная стоимость может меняться в течение периода ее полного погашения.

Дюрация позволяет инвестору в полной мере оценить финансовую привлекательность облигаций на рынке ценных бумаг, учитывая сразу несколько важных показателей — срок, на который выдана облигация, ставку процента (купон), номинальную стоимость ценной бумаги. Вычисленный показатель дюрации облигации поможет инвесторам принять решение о размещении портфеля ценных бумаг с наибольшей прибылью.

Расчет дюрации ценной бумаги может быть произведен несколькими способами:

Формула дюрации — как подсчитать значение

Дюрация зависит от трех составляющих: цена, процентная ставка и срока до погашения

De = /

Где:

• De – значение эффективной дюрации облигации
• Pi- – рыночная цена при понижении ставки
• Pi+ – рыночная цена при возрастании ставки
• Pr – номинальная цена ценной бумаги
• i+ – повышенная стартовая ставка
• i— – сниженная стартовая ставка

Считать самостоятельно дюрацию облигации по формуле не нужно. Она уже подсчитана автоматически. Данные можно посмотреть в торговом терминале QUIK или в открытых источниках по облигациям: https://www.rusbonds.ru (например).

Сложность формулы заключается в том, что текущие деньги не равны завтрашним деньгам. Поэтому для точности расчётов их следует дисконтировать.

Есть также другая формула дюрации, которая учитывает еще и ставку дисконтирования:

D = / (1+i)t) + ( / (1+i)n)] / p

Где:

• n – число платежей
• t – период, требуемый для полного погашения
• M – погашение номинальной цены облигации
• C – денежные поступления процентной прибыли
• i – ставка дисконтирования
• p – рыночная цена облигации

Дюрация Маколея

Фредерик Маколей вывел формулу вычисления дюрации еще в 30-х годах прошлого столетия, однако практическое использование в России ее началось только с 1993 г.

Формула выглядит следующим образом:

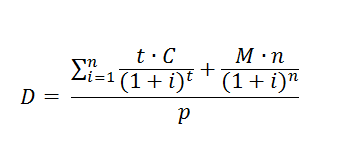
• где D – дюрация,
• n – количество платежей,
• t – время, необходимое для полного погашения,
• M – погашение номинальной стоимости ценной бумаги,
• С – денежный поток процентных доходов,
• i – ставка дисконтирования,
• p – рыночная стоимость ценной бумаги

К примеру, инвестор имеет две облигации номинальной стоимостью 5000 рублей каждая, при этом одна из них с нулевым купоном (бескупонная) и сроком погашения 3 года, другая с купоном, равным 5 %, который выплачивается ежегодно, сроком погашения также 3 года.

В первом случае дюрация будет равна сроку погашения облигации, а именно 3 года, так как денежный поток процентных доходов равен 0.

Во втором случае расчет можно произвести следующим образом:

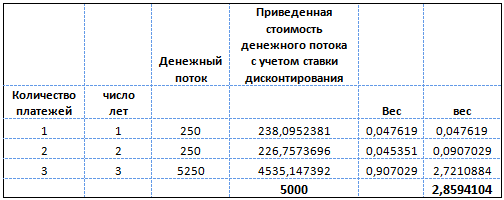
Дюрация облигации с 5 % купоном составит 2,86 года.

Модифицированная дюрация

В случае если процентная ставка доходности меняется в каком-либо временном промежутке до момента полного погашения номинальной стоимости, то необходимо использовать для расчета формулу модифицированной дюрации:

Dm= D/(1+ Cm/n)

• где Dm – модифицированная дюрация,
• Cm – доходность до погашения,
• n – количество выплат по купонам в год

Применяя предыдущий расчет, вычислим Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72

Таким образом, при увеличении дохода по купону, дюрация снижается.

Однако, модифицированная дюрация применима лишь в том случае, если доходные денежные потоки с изменением процентной ставки не меняются, что в практическом применении чаще всего невозможно. Для расчета необходим более чувствительный инструмент к колебаниям ставки процента и, соответственно, доходности, каким и является эффективная дюрация.

Эффективная дюрация

При расчете эффективной дюрации облигации учитываются колебания процентных ставок как в сторону уменьшения, так и в сторону увеличения. Формула для расчета выглядит следующим образом:

• Где De – эффективная дюрация,
• Pi- — стоимость облигации при уменьшении процентной ставки,
• Pi+ — стоимость облигации при увеличении процентной ставки,
• Ро – начальная стоимость облигации,
• i+ — увеличенная начальная процентная ставка,
• i- — уменьшенная начальная процентная ставка.

Расчет эффективной дюрации применим с использование биноминального процентного дерева для исчисления стоимости облигации с учетом колебаний процентных ставок.

Немного про банки и кредиты

Кстати приведенные выше примеры вполне объясняют почему банки дают кредиты и требуют погашать долг с процентами каждый месяц.

Как вы поняли — это один из главных способов минимизации рисков от невозврата. Зачем давать кредит с условием возврата полной суммы с процентами в конце срока? И ждать несколько лет, когда можно сразу же получать заемные средства частями.

Аналогично действует и процентная ставка на выдаваемые кредиты. Для каждого клиента она варьируется. Ненадежные (с точки зрения банка) заемщики получают кредит с более высокими процентами. По сравнению с платежеспособным потоком постоянных клиентов.

Риск невозврата в первом случае гораздо выше.  И дабы примерно уравновесить риски по выданным кредитам в обоих категориях заемщиков, банки повышают ставки (снижают риски) для категории ненадежных.

Переводя на облигации, являющиеся долговыми расписками или кредитом, которые вы даете эмитенту, выпускающему бумагу получаем.

ДРУГИЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ С ПРИМЕНЕНИЕМ ДЮРАЦИИ

   Мы уже писали о том, что применять дюрацию в качестве единственной меры волатильности цены облигации неразумно. Ниже мы обратимся к двум другим особенностям использования понятия дюрации в инвестиционной практике.   Напомним, что, выясняя характер зависимости между модифицированной дюрацией и волатильностью цены облигации, мы начали анализ с ценового уравнения (4.1). Данная формула предполагает, что все денежные потоки облигации дисконтированы по единой дисконтной ставке (целесообразность этого предположения мы обсуждаем в главе 5, говоря о кривой доходности). В целом, как формула (4.3), так и ее варианты строятся на основании утверждения о том, что кривая доходности является плоской и изменения доходности в любой ее части параллельны. В главе 19 мы доказываем, что применение дюрации в ситуации, когда изменения доходности в разных частях кривой не параллельны, дает не слишком надежный результат

Это особенно важно помнить инвесторам, пытающимся с помощью значения портфельной дюрации выяснить степень чувствительности стоимости портфеля к изменению процентных ставок. Если в портфель входят облигации с различными длительностями, дюрация, как правило, не учитывает неодинаковые изменения процентных ставок для различных длительностей

В конце этой главы мы предложим один из возможных способов измерения чувствительности портфеля в ситуации, когда процентные ставки для разных длительностей меняются на разное число базисных пунктов.   Второе положение, которое следует помнить инвесторам, работающим с понятием дюрации: все выводы, сделанные нами в этой главе, имеют отношение только к облигациям без встроенных опционов. Если изменение доходностей приводит к изменениям предполагаемых денежных потоков облигации (а именно так происходит с облигациями, имеющими встроенные опционы), меры дюрации и выпуклости применимы лишь в некоторых специфических случаях. Волатильность цен облигаций со встроенными опционами мы анализируем в главах 17 и 18.   Мера дюрации, о которой пойдет речь в этих главах, т. е. дюрация, принимающая в расчет встроенные опционы, получила название эффективной дюрации.

Дюрация облигации: расчет, формула

Величина дюрации может быть использована для характеристики многих инвестиционных инструментов, но чаще всего ее применяют для учета рисков при использовании ценных бумаг с установленным сроком обращения.

Наиболее распространенным использованием показателя дюрации является расчет дюрации облигации. Как уже было приведено выше, дюрация облигации идентична общему понятию дюрации, что представляет собой определенное количество лет, необходимое на погашение полной стоимости облигации.

Облигация является эмиссионной долговой ценной бумагой и ее рыночная стоимость может меняться в течение периода ее полного погашения.

Дюрация позволяет инвестору в полной мере оценить финансовую привлекательность облигаций на рынке ценных бумаг, учитывая сразу несколько важных показателей — срок, на который выдана облигация, ставку процента (купон), номинальную стоимость ценной бумаги. Вычисленный показатель дюрации облигации поможет инвесторам принять решение о размещении портфеля ценных бумаг с наибольшей прибылью.

Расчет дюрации ценной бумаги может быть произведен несколькими способами:

Дюрация Маколея

Фредерик Маколей вывел формулу вычисления дюрации еще в 30-х годах прошлого столетия, однако практическое использование в России ее началось только с 1993 г.

Формула выглядит следующим образом:

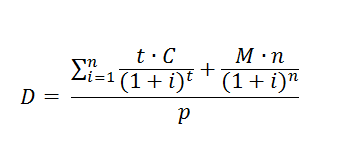
• где D – дюрация,
• n – количество платежей,
• t – время, необходимое для полного погашения,
• M – погашение номинальной стоимости ценной бумаги,
• С – денежный поток процентных доходов,
• i – ставка дисконтирования,
• p – рыночная стоимость ценной бумаги

К примеру, инвестор имеет две облигации номинальной стоимостью 5000 рублей каждая, при этом одна из них с нулевым купоном (бескупонная) и сроком погашения 3 года, другая с купоном, равным 5 %, который выплачивается ежегодно, сроком погашения также 3 года.

В первом случае дюрация будет равна сроку погашения облигации, а именно 3 года, так как денежный поток процентных доходов равен 0.

Во втором случае расчет можно произвести следующим образом:

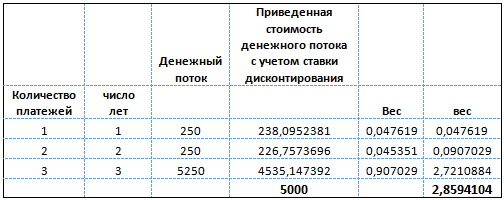
Дюрация облигации с 5 % купоном составит 2,86 года.

Модифицированная дюрация

В случае если процентная ставка доходности меняется в каком-либо временном промежутке до момента полного погашения номинальной стоимости, то необходимо использовать для расчета формулу модифицированной дюрации:

Dm= D/(1+ Cm/n)

• где Dm – модифицированная дюрация,
• Cm – доходность до погашения,
• n – количество выплат по купонам в год

Применяя предыдущий расчет, вычислим Dm= 2.86/((1+0.05/1))=2.86/1.05=2.72

Таким образом, при увеличении дохода по купону, дюрация снижается.

Однако, модифицированная дюрация применима лишь в том случае, если доходные денежные потоки с изменением процентной ставки не меняются, что в практическом применении чаще всего невозможно. Для расчета необходим более чувствительный инструмент к колебаниям ставки процента и, соответственно, доходности, каким и является эффективная дюрация.

Эффективная дюрация

При расчете эффективной дюрации облигации учитываются колебания процентных ставок как в сторону уменьшения, так и в сторону увеличения. Формула для расчета выглядит следующим образом:

• Где De – эффективная дюрация,
• Pi- — стоимость облигации при уменьшении процентной ставки,
• Pi+ — стоимость облигации при увеличении процентной ставки,
• Ро – начальная стоимость облигации,
• i+ — увеличенная начальная процентная ставка,
• i- — уменьшенная начальная процентная ставка.

Расчет эффективной дюрации применим с использование биноминального процентного дерева для исчисления стоимости облигации с учетом колебаний процентных ставок.

Дюрация облигации на простом примере

Специалисты американского инвестиционного банка Salomon Brothers предлагают рассмотреть дюрацию на следующем простом примере. Давайте представим, что все выплаты по облигации – это стаканы, которые находятся на деревянной качели. При этом расстояние между предметами одинаковое. В данном случае промежуток между станками следует рассматривать в качестве периодичности, которая установлена для платежей по ценным бумагам.

Возьмем за точку отсчета место опоры качели, которое позволяет доске удерживать баланс. Дюрацию будет, собственно, составлять расстояние от точки опоры до края доски вместе с расположенными на ней стаканами.

В действительности дюрация характеризуется как варьирование стоимости в процентном соотношении на определенном промежутке времени. Изменение доходности составляет 1%.

Например, при дюрации с трехлетним сроком можно ожидать, что изменение курса облигации будет равно 3%, в то время как изменение доходности – всего лишь 1%.

Следует различать дюрацию бескупонных облигаций и дюрацию купонных. Во втором случае величина дюрации будет меньше периода погашения долговой бумаги. Если была приобретена бескупонная облигация, то срок погашения будет однозначно равен показателю дюрации.

Модифицированная дюрация

Не бойтесь, заумных слов говорить не буду. Быстро на пальцах объясню вкратце что это такое.

У наших «подопытных» модифицированная дюрация всего портфеля составляет:

• FXFA — 7,87;
• VTBH — 3.67.

Выше я писал, что купонная доходность фондов (после вычета комиссий) составляет 2.8 (FXFA) и 3.3 (VTBH) годовых.

Как это работает?

Смоделируем ситуацию:

Допустим вы решили вложиться в FXFA.

Ваша суммарная купонная доходность за 3 года составит (очень грубо): FXFA = 8.1% (3 года х 2.7%).

Через 3 года ФРС повышает процентную ставку на 1%. Стоимость портфеля облигаций снизится на 7,87%. Получается по факту вы заработали 0.23% чистой прибыли (8.1% — 7,87%). ЗА ТРИ ГОДА. Соответственно при росте ставки на большее значение (1,5% — 2%) — мы сразу уходим в минус.

Обычно ФРС меняет ставку по 0.25 п.п. — и каждое такое увеличение будет в среднем снижать стоимость бумаг примерно на 2%.

Что у нас по VTBH?

За счет более низкой модифицированной дюрации портфеля (3,67), зависимость от процентных ставок будет ниже (капитан Очевидность).

При тех же условиях: за 3 года за счет купонного дохода БПИФ VTBH даст прибавку в 9.9% прибыли. Рост ставок на 1% — обвалит котировки на 3.67%. В итоге у нас останется на руках — +6,2% прибыли.

Выпуклость облигаций

Для обычного частного инвестора объем приведенный выше информации вполне достаточен, чтобы управлять процентным риском небольшого портфеля, используя дюрацию

Но для более точных расчетов, важность которых возрастает с ростом суммы и сроков инвестиций, необходимо познакомиться еще с одним понятием. Модифицированная дюрация дает только приблизительную оценку и подходит лишь для небольших изменений доходности

Зависимость цены облигации от ее доходности не линейная, а выпуклая.

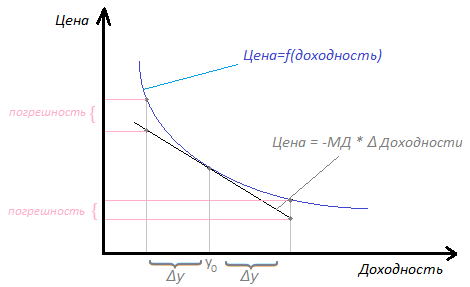график выпуклости

Выпуклость облигаций бывает позитивной и негативной, а точное значение выпуклости для конкретных облигаций можно посмотреть на rusbonds. В некоторых источниках выпуклость называют конвекцией.

Таким образом, чем больше изменение процентной ставки, тем больше реальное изменение стоимости будет отклоняться от расчетного. Диапазон ставок, в котором погрешность можно считать несущественной, зависит от параметров конкретной облигации и объема средств, которые планируется в нее инвестировать.
Математический смысл выпуклости выходит за рамки этой статьи, но для практического применения обычному частному инвестору он, в общем-то, ни к чему. Значение выпуклости можно найти на тех же специализированных ресурсах вроде rusbonds.ru или cbonds.ru.

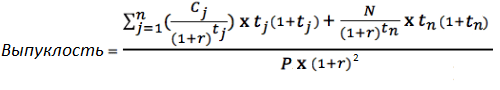Формула выпуклости

Вот главное, что нужно понимать о выпуклости:

1. Одновременное использование дюрации и выпуклости дает более корректное значение изменения доходности облигации в ответ на смещение процентных ставок.
2. При прочих равных большая выпуклость более выгодна для инвестора.

Выпуклость портфеля облигаций измеряется аналогично дюрации портфеля: выпуклость каждой бумаги умножается на её вес в портфеле и полученные значения складываются.

Формула выпуклости портфеля

Приведенные показатели дюрации и выпуклости справедливы только для обыкновенных облигаций без встроенных опционов. Если изменение доходностей приводит к изменениям предполагаемых денежных потоков облигации, то меры дюрации и выпуклости применимы лишь в некоторых специфических случаях.

Дюрация Маколея: формула расчета

Наиболее популярным способом расчета является формула дюрации Маколея. На международных рынках средневзвешенный эффективный срок окупаемости долговых бумаг определяется в годах, на российском рынке – в днях.

Формула дюрации по Маколею выглядит следующим образом:

\

D – дюрация;

n – количество платежей;

t – время до погашения;

M – номинальная стоимость;

C – денежный поток с учетом НКД;

i – ставка дисконтирования;

p – текущая рыночная стоимость.

Пример. Номинальная стоимость облигации – 1 500 руб. (20 $ или 580 грн.), срок погашения – 2 года. Купон – 10 %, выплаты – раз в год (150 руб. (2 $ или 58 грн.)). Рыночная цена – 1 875 руб. (25 $ или 725 грн.).

\

Какие бывают ОФЗ

Вид облигации зависит от её купона. Он может быть фиксированный и переменный. Ставка фиксированного купона всегда одинаковая, а ставка переменного купона меняется перед каждым периодом и зависит от ставки RUONIA — рекомендательной, но не обязательной ставки однодневных рублёвых кредитов. Её называют индикативной ставкой. Это средняя ставка, по которой крупнейшие российские банки выдают кредиты друг другу на один день. Она очень близка к ключевой ставке. Значения RUONIA можно узнать на сайте Банка России.

Виды облигаций обозначают цифрами. Например, в ОФЗ 25083 первые две цифры — это вид, облигации с переменным купоном. Мы указали обозначения вида в скобках.

ОФЗ-ПК (26, 25) — облигации с переменным купоном. Чем выше ставка RUONIA, тем выше доходность ОФЗ-ПК.

Купон по ОФЗ-ПК — это среднее значение RUONIA за определенный период + фиксированная премия. Если ставка RUONIA меняется, то размер купона меняется тоже, и так вплоть до самого погашения. Выплаты по таким купонам могут быть 2−4 раза в год.

Доход инвестора — это переменный купон. Есть отдельный вид ОФЗ, у которых доходность привязана к инфляции — ОФЗ-ИН. Но в основном инвесторы используют облигации ПК, чтобы обезопасить себя от изменения ставки в сторону повышения. Обычно при росте ставки цена облигации падает и инвестор оказывается в убытке, а в облигациях ПК по-другому: доходность в следующем купоне после повышения ставки начнёт приближаться к её новому значению плюс премия. Если ставка снизится, то купон ПК тоже уменьшится, но всё же будет чуть выше за счёт премии.

ОФЗ-ПД (29) — облигации с постоянным купонным доходом. Минфин заранее обозначает ставку купона, например 7,85 % от номинала. Если номинал облигации 1000 ₽, размер купона будет 78,5 ₽ в год.

Инвестор купил 10 ОФЗ-ПД номиналом 1000 ₽ со сроком погашения 5 лет. Купонная ставка — 7,85 % годовых. Когда он предъявит облигации к погашению, то получит 3 925 ₽ купонного дохода (7,85 % х 5) и 10 000 ₽ за номинал облигаций. Итого 13 925 ₽. Конечно, с этих денег удержат комиссию, но это уже совсем другая история.

ОФЗ-ФД — облигации с фиксированным купонным доходом. Если постоянный купонный доход не меняется на протяжении всей «жизни» облигации, то фиксированный купонный доход меняться может, но на некоторый период. Например, сначала ставка будет 6 %, затем 5 %. При покупке облигаций купонный доход уже будет известен. Срок обращения таких облигаций больше 4 лет, а частота выплат по купону 4 раза в год.

Инвестор купил 10 ОФЗ-ФД номиналом 1000 ₽. Каждый год ставка купона чередуется: сначала 5 %, затем 6 %. За 5 лет инвестор получит такую прибыль: 10 000 ₽ + 500 ₽ + 600 ₽ + 500 ₽ + 600 ₽ + 500 ₽ = 12 700 ₽.

ОФЗ-АД (46, 48) — облигации с амортизацией долга. Эмитент не только платит по купонам, но и частично погашает долг. Эти облигации не слишком доходны, но если прогнозируется значительное увеличение процентных ставок, то ОФЗ-АД покупать выгодно. Владелец будет получать часть номинала и реинвестировать эти деньги в новые облигации.

Если вы хотите периодически пользоваться деньгами, но не хотите продавать активы, то такие ОФЗ тоже пригодятся, но встречаются они редко.

ОФЗ-ИН (51, 52) — облигации с индексируемым номиналом. Номинал индексируется на размер инфляции — если она растёт, то и номинал увеличивается. Когда закончится срок обращения, Минфин вернет сумму, проиндексированную на день возврата. Если же инфляция окажется отрицательной, Минфин всё равно вернёт не меньше 1000 ₽.

ОФЗ-н — «народные» облигации. Они выпущены специально, чтобы купить облигации мог любой желающий. Брокерский счёт при этом все равно нужен. ОФЗ-н не торгуются на бирже, их можно купить в банках, например в ВТБ, «Промсвязьбанке», «Сбербанке», «Почта Банке». Эти облигации выпускают на 3 года, потом они автоматически погашаются. Минимальная сумма покупки — 10 000 ₽.

ОФЗ-н можно досрочно погасить по номиналу. Если сделать это в течение первого года владения, то выплаченный и купонный доход будет потерян. Если после первого года владения — то доход сохранится. Подробнее узнать и купить облигации можно в приложении ВТБ Мои Инвестиции.

Пример по конкретному текущему выпуску ОФЗ-н
Купонный доход платят раз в полгода. Купонная ставка:

• первый купон — 4,10 % годовых;
• второй купон — 4,40 % годовых;
• третий купон — 4,70 % годовых;
• четвёртый купон — 5,00 % годовых;
• пятый купон — 5,30 % годовых;
• шестой купон — 5,73 % годовых.

Если вы купите облигации на 10 000 ₽, то вместе с номиналом получите назад 11 460 ₽.

Дюрация некоторых потоков платежей

Дюрация аннуитета

Можно показать, что дюрация аннуитета, ограниченного сроком T, равна следующей величине:

Модифицированную дюрацию можно получить разделением на .

Здесь в формуле подразумевается эффективная ставка за интервал аннуитета и срок и дюрацию также в интервалах аннуитета. Если использовать годовую эффективную ставку, то для дюрации в годах формула будет такой

где — длительность интервала аннуитета в годах (доля года), — срок аннуитета в годах, — годовая эффективная ставка. При t=1 получаем прежнюю формулу.

Для вечного аннуитета формулу дюрации можно определить как предел приведенной формулы при (второе слагаемое в этом случае будет стремиться к нулю). Можно также вывести формулу непосредственно. Приведенная стоимость вечного аннуитета равна . Воспользуемся формулой через производную. Производная этой функции по , очевидно равна . Умножая эту величину на и разделив на , получим окончательно формулу дюрации:

Модифицированная дюрация, очевидно равна в этом случае .

Дюрация облигации

Для бескупонной облигации номиналом со сроком погашения текущая стоимость равна

Она же совпадает с дисконтированной стоимостью единственного платежа, поэтому её дюрация просто равна сроку облигации:

В случае купонной облигации денежный поток состоит из купонных платежей и погашения номинала. При этом погашение номинала может быть частями (амортизация) и купонная ставка может, вообще говоря, изменяться в течение срока обращения облигации. Если величину купонов обозначить , а погашения номинала , то дюрация облигации будет равна

где  — цена облигации (предполагается что в качестве используется доходность к погашению облигации, поэтому ).

Формула будет иметь точно такой же вид, если вместо величины купонов использовать соответствующие купонные ставки, вместо сумм погашений номинала  — доли погашений номинала, а вместо цены облигации в денежном выражении использовать стандартную цену в процентах (долях) от номинала.

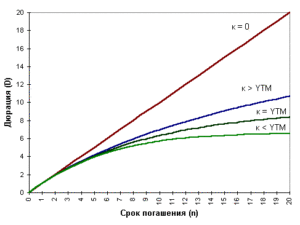
При прочих равных условиях, чем больше срок погашения и (или) ниже купонная ставка и (или) ниже доходность к погашению, тем больше дюрация облигации. При прочих равных условиях чем чаще выплачивается купон, тем меньше дюрация.

В простейшем случае постоянной купонной ставки и единовременного погашения номинала в конце срока для расчета дюрации можно использовать встроенную в Microsoft Office Excel 2007 функцию ДЛИТ.