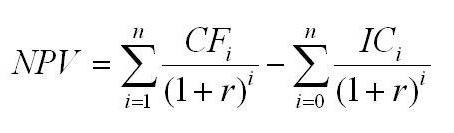Чистая приведенная стоимость (npv). расчет чистой приведенной стоимости

Пример

Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет.
Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.

Таким образом, требуется оценить, какая сумма больше:

100000⋅(1+0.1)t≶∑i=1tpi⋅(1+0.1)(t−i){\displaystyle 100\,000\cdot (1+0.1)^{t}\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(t-i)}}, где pi{\displaystyle p_{i}} — доход от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на (1+0.1)t{\displaystyle (1+0.1)^{t}}:

100000≶∑i=1tpi⋅(1+0.1)(−i){\displaystyle 100\,000\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(-i)}}.

Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:

Год	Денежный поток	Приведённая стоимость
T=0	−100000(1+0.10){\displaystyle {\frac {-100\,000}{(1+0.10)^{0}}}}	– $ 100 000
T=1	30000−5000(1+0.10)1{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{1}}}}	$ 22 727
T=2	30000−5000(1+0.10)2{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{2}}}}	$ 20 661
T=3	30000−5000(1+0.10)3{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{3}}}}	$ 18 783
T=4	30000−5000(1+0.10)4{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{4}}}}	$ 17 075
T=5	30000−5000(1+0.10)5{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{5}}}}	$ 15 523
T=6	30000−5000(1+0.10)6{\displaystyle {\frac {30\,000-5000}{(1+0.10)^{6}}}}	$ 14 112

Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.

Тот же пример с формулами в Excel:

• NPV (ставка, net_inflow) + initial_investment
• PV (ставка, year_number, yearly_net_inflow)

При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.

Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу

1−(1+i)−ni{\displaystyle {\frac {1-(1+i)^{-n}}{i}}} мы получим 1−(1+0.1)−60.1=4.3553{\displaystyle {\frac {1-(1+0.1)^{-6}}{0.1}}=4.3553}.

И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):

4.3553(30000−5000)−100000=$8881.52{\displaystyle -100\,000=\$\,8\,881.52}

Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.

Understanding Net Present Value

NPV looks to assess the profitability of a given investment on the basis that a dollar in the future is not worth the same as a dollar today. Money loses value over time due to inflation. However, a dollar today can be invested and earn a return, making its future value possibly higher than a dollar received at the same point in the future. NPV seeks to determine the present value of an investment’s future cash flows above the investment’s initial cost. The discount rate element of the NPV formula discounts the future cash flows to the present-day value. If subtracting the initial cost of the investment from the sum of the cash flows in the present-day is positive, then the investment is worthwhile.

For example, an investor could receive $100 today or a year from now. Most investors would not be willing to postpone receiving $100 today. However, what if an investor could choose to receive $100 today or $105 in one year? The 5% rate of return (RoR) for waiting one year might be worthwhile for an investor unless another investment could yield a rate greater than 5% over the same period.

If an investor knew they could earn 8% from a relatively safe investment over the next year, they would choose to receive $100 today and not the $105 in a year, with the 5% rate of return. In this case, 8% would be the discount rate.

Positive vs. Negative NPV

A positive NPV indicates that the projected earnings generated by a project or investment—in present dollars—exceeds the anticipated costs, also in present dollars. It is assumed that an investment with a positive NPV will be profitable.

An investment with a negative NPV will result in a net loss. This concept is the basis for the Net Present Value Rule, which dictates that only investments with positive NPV values should be considered.

Преимущества и недостатки

Достоинства метода заключаются в следующем:

1. NPV учитывает временной фактор – изменение стоимости денег и длительность жизненного цикла инвестиционного проекта.
2. В немалой степени отражает основные критерии эффективности инвестиций: оценка рисков, расчет срока окупаемости и разницы между доходами и расходами с учетом инфляции.

Недостатки:

Спрогнозировать денежные потоки непросто – всегда найдутся факторы, которые невозможно принять во внимание заранее.
Сложный механизм расчета ставки дисконтирования. Точнее, сложность не в формуле ее расчета, а в выборе правильного метода

Выбрав неподходящий метод, можно получить значение NPV, далекое от истины.

Расчет чистого дисконтированного дохода

Показатель чистого дисконтированного дохода (ЧДД) по-английски называется Net present value, поэтому общепринято сокращенно его называть NPV. Существует ещё альтернативное его наименование – Чистая приведенная стоимость.

NPV определяет сумму приведенных к нынешнему дню дисконтированных значений платежей, которые являются разностью между притоками и оттоками. Если говорить простым языком, то данный показатель определяет, какую сумму прибыли планирует получить инвестор за вычетом всех оттоков после того, как окупится первоначальный вклад.

В программе Excel имеется функция, которая специально предназначена для вычисления NPV. Она относится к финансовой категории операторов и называется ЧПС. Синтаксис у этой функции следующий:

Аргумент «Ставка» представляет собой установленную величину ставки дисконтирования на один период.

Аргумент «Значение» указывает величину выплат или поступлений. В первом случае он имеет отрицательный знак, а во втором – положительный. Данного вида аргументов в функции может быть от 1 до 254. Они могут выступать, как в виде чисел, так и представлять собой ссылки на ячейки, в которых эти числа содержатся, впрочем, как и аргумент «Ставка».

Проблема состоит в том, что функция хотя и называется ЧПС, но расчет NPV она проводит не совсем корректно. Связано это с тем, что она не учитывает первоначальную инвестицию, которая по правилам относится не к текущему, а к нулевому периоду. Поэтому в Экселе формулу вычисления NPV правильнее было бы записать так:

Естественно, первоначальная инвестиция, как и любой вид вложения, будет со знаком «-».

Пример вычисления NPV

Давайте рассмотрим применение данной функции для определения величины NPV на конкретном примере.

1. Выделяем ячейку, в которой будет выведен результат расчета NPV. Кликаем по значку «Вставить функцию», размещенному около строки формул.

Запускается окошко Мастера функций. Переходим в категорию «Финансовые» или «Полный алфавитный перечень». Выбираем в нем запись «ЧПС» и жмем на кнопку «OK».

После этого будет открыто окно аргументов данного оператора. Оно имеет число полей равное количеству аргументов функции. Обязательными для заполнения является поле «Ставка» и хотя бы одно из полей «Значение».

В поле «Ставка» нужно указать текущую ставку дисконтирования. Её величину можно вбить вручную, но в нашем случае её значение размещается в ячейке на листе, поэтому указываем адрес этой ячейки.

В поле «Значение1» нужно указать координаты диапазона, содержащего фактические и предполагаемые в будущем денежные потоки, исключая первоначальный платеж. Это тоже можно сделать вручную, но гораздо проще установить курсор в соответствующее поле и с зажатой левой кнопкой мыши выделить соответствующий диапазон на листе.

Так как в нашем случае денежные потоки размещены на листе цельным массивом, то вносить данные в остальные поля не нужно. Просто жмем на кнопку «OK».

Расчет функции отобразился в ячейке, которую мы выделили в первом пункте инструкции. Но, как мы помним, у нас неучтенной осталась первоначальная инвестиция. Для того, чтобы завершить расчет NPV, выделяем ячейку, содержащую функцию ЧПС. В строке формул появляется её значение.

После символа «=» дописываем сумму первоначального платежа со знаком «-», а после неё ставим знак «+», который должен находиться перед оператором ЧПС.

Можно также вместо числа указать адрес ячейки на листе, в которой содержится первоначальный взнос.

Для того чтобы совершить расчет и вывести результат в ячейку, жмем на кнопку Enter.

Результат выведен и в нашем случае чистый дисконтированный доход равен 41160,77 рублей. Именно эту сумму инвестор после вычета всех вложений, а также с учетом дисконтной ставки, может рассчитывать получить в виде прибыли. Теперь, зная данный показатель, он может решать, стоит ему вкладывать деньги в проект или нет.

Урок: Финансовые функции в Excel

Как видим, при наличии всех входящих данных, выполнить расчет NPV при помощи инструментов Эксель довольно просто. Единственное неудобство составляет то, что функция, предназначенная для решения данной задачи, не учитывает первоначальный платеж. Но и эту проблему решить несложно, просто подставив соответствующее значение в итоговый расчет.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Существующие методы оценки

Методы оценки эффективности инвестиций являются краеугольным камнем в работе любого профессионального инвестора. Без них невозможно себе представить осуществление успешных вложений. С помощью разработанных методик можно отследить реальную эффективность использования инвестируемого капитала.

Зачастую в финансовой литературе принято выделять четыре основные группы подобных методов.

1. В первом случае оценка эффективности инвестиций производится с использованием соотношения значений расходов и доходов.

2. Статистические методы, которые применяются при краткосрочном характере инвестиционных проектов.

3. Динамические методы, которые учитывают фактор влияния времени. В качестве примера можно привести вычисление эффективности инвестиций с учетом временной стоимости денег.

4. Способы, в которых эффективность инвестиционной деятельности определяется исходя из проведения анализа бухгалтерской отчетности за интересующий период.

Помимо этого, существуют 3 разновидности оценки эффективности:

• экономическая;
• бюджетная;
• финансовая.

Экономическая оценка эффективности вложений иллюстрирует собой существующую разницу между расходной и доходной частью проекта.

Бюджетная оценка эффективности произведенных инвестиций показывает финансовые результаты для бюджетов разного уровня.

Финансовая оценка рассматривает результативность осуществленного инвестиционного проекта с точки зрения инвестора.

Конкретные методики инвестиционного анализа подбираются в зависимости от реально существующего процесса инвестирования. С помощью применения существующих методов можно осуществить детальный инвестиционный анализ. Выявленная эффективность инвестиций поможет правильно выбрать наиболее привлекательный объект для вложения денег.

Что такое NPV или чистый дисконтированный доход

Это показатель, который отражает размер денежных потоков в течение периода их реализации. Он также показывает величину, приведенную к текущей цене (дисконтирование). При помощи такого показателя рассчитывается разница между возвратными потоками средств и исходными вложениями. Формула чистого дисконтированного дохода позволяет сделать вывод, насколько эффективно вложение средств в определенное направление деятельности. После проведенных вычислений становится понятно, сколько оттоков и поступлений было приведено за обозначенное время. В результате руководитель видит, оправданно ли инвестирование проекта.

NPV позволяет выяснить эффективность вложенных средств

Смысл показателя

Его задача – дать представление об оправданности запланированных вложений. Этот параметр позволяет сравнить несколько проектов, куда инвестор планирует внести деньги, выявить их прибыльность и определиться с объектом инвестирования. Как только он выбран, возможно вычислить npv инвестиционного проекта – что это? Так называется приведенная чистая цена всех финансов, связанных с определенным проектом. Данный показатель выполняет несколько функций. При помощи него:

• устанавливается прибыльность предприятия, куда вкладываются деньги;
• определить целесообразность дела;
• выявить оптимальный срок инвестирования;
• оценить степень убытка от сделанных вложений.

Благодаря вычислению данного параметра инвестор сможет спрогнозировать, сколько материальных средств он потеряет и приобретет в будущем. Если число потерь велико, он примет решение о выборе иного объекта для вложения денег. Выбор в пользу источника финансирования делается, исходя из технологических, организационных и финансовых аспектов. Однако в ряде случаев все зависит от иностранных факторов. Тогда учитывается конкурентность и востребованность определенного сегмента на рынке.

Тонкости расчета NPV

Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала, то вы легко сможете подставить их в формулу и рассчитать NPV. Но на практике не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.

Денежные потоки

Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.

Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.

Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.

Ставка дисконтирования

Ставка дисконтирования в формуле расчета NPV — это стоимость капитала для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы. В общем случае компания может получить финансирование из трех источников:

• взять в долг (обычно у банка);
• продать свои акции;
• использовать внутренние ресурсы (например, нераспределенную прибыль).

Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств. Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.

Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV)  будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC (Weighted Average Cost of Capital), что переводится как средневзвешенная стоимость капитала.

Два способа посчитать NPV в Excel

Я назову героем того, кто рассчитает такую формулу на листочке. Excel в помощь обычным людям:

1. Создать таблицу, в ее верхней части занести по периодам суммы инвестиций, расходов и доходов по проекту.
2. Рассчитать чистый денежный поток.

Дальше выбрать один из способов расчета:

1. Занести i для проекта по периодам. Разбить формулу на блоки и последовательно рассчитать до конечного результата. На примере показана следующая последовательность: начала знаменатель, затем дисконтированный денежный поток за период. Суммировать полученные результаты.

Этот способ имеет свои преимущества, он больше подходит, если:

• нужно видеть промежуточные результаты;
• ставка дисконтирования в различные периоды отличается.

1. Использовать встроенную формулу Excel. Выбрать в блоке финансовых формул – она называется ЧПС. Заполнить поля: ставка дисконтирования и диапазон суммирования (значения чистого денежного потока по периодам).

Ниже я покажу, что результаты при единой ставке дисконтирования на все периоды совпадают.

Расчет NPV. Пример

Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:
где

• n, t — количество временных периодов;
• CF — денежный поток (англ. Cash Flow);
• R — стоимость капитала, она же ставка дисконтирования (англ. Rate).

На самом деле эта формула —  всего лишь правильное математическое представление суммирования нескольких величин. Чтобы  рассчитать NPV, возьмем для примера два проекта A и B, которые имеют следующую структуру денежных потоков на ближайшие 4 года:

Таблица 1. Денежный поток проектов A и B.

Год	Проект A	Проект B
($10,000)	($10,000)
1	$5,000	$1,000
2	$4,000	$3,000
3	$3,000	$4,000
4	$1,000	$6,000

Оба проекта A и B имеют одинаковые первоначальные инвестиции в $10,000, но денежные потоки в последующие годы сильно разнятся. Проект A предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект B, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта A, но зато в последующие два года Проект B принесет больше денежных средств, чем проект A. Рассчитаем NPV инвестиционного проекта.

Для упрощения расчета предположим:

• все денежные потоки случаются в конце каждого года;
• первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас;
• стоимость капитала (ставка дисконтирования) составляет 10%.

Напомним, что для того, чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».

Применим формулу NPV для Проекта A. У нас четыре годовых периода и пять денежных потоков. Первый поток ($10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:

Если подставить в эту сумму данные из таблицы для Проекта A вместо CF и ставку 10% вместо R, то получим следующее выражение:

То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока. В результате приведенная стоимость денежных потоков для проекта A равна $788,2. Расчет NPV для проекта A можно так же представить в виде таблицы и в виде шкалы времени:

Таблиц 2. Расчет NPV для проекта A.

Год	Проект A	Ставка 10%	Фактор	Сумма
($10,000)	1	1	($10,000)
1	$5,000	1 / (1.10)1	0.9091	$4,545.5
2	$4,000	1 / (1.10)2	0.8264	$3,305.8
3	$3,000	1 / (1.10)3	0.7513	$2,253.9
4	$1,000	1 / (1.10)4	0.6830	$683.0
ИТОГО:	$3,000			$788.2

Рисунок 1. Расчет  NPV для проекта А.

Аналогичным образом рассчитаем NPV для проекта B.

Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших ($4,000 и $6,000), но отдалённых по времени (годы 3 и 4) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта B чистая приведенная стоимость денежных потоков будет меньше, чем для проекта A. Наши расчеты NPV для проекта B дали результат — $491,5. Детальный расчет NPV для проекта B показан ниже.

Таблиц 2. Расчет NPV для проекта A.

Год	Проект B	Ставка 10%	Фактор	Сумма
($10,000)	1	1	($10,000)
1	$1,000	1 / (1.10)1	0.9091	$909.1
2	$3,000	1 / (1.10)2	0.8264	$2,479.2
3	$4,000	1 / (1.10)3	0.7513	$3,005.2
4	$6,000	1 / (1.10)4	0.6830	$4,098.0
ИТОГО:	$4,000			$491.5

Рисунок 2. Расчет  NPV для проекта B.

Вывод

Оба эти проекта можно принять, так как NPV обоих проектов больше нуля, а, значит осуществление этих проектов приведет к увеличению доходов компании-инвестора. Если эти проекты взаимоисключающие и необходимо выбрать только один из них, то предпочтительнее выглядит проект A, поскольку его NPV=$788,2, что больше NPV=$491,5 проекта B.

Варианты вложений

Существует три способа распоряжения денежными средствами проекта: расходование, сбережение, инвестиционный. Самым простым, но не самым доходным вариантом является вложение средств в банк, покупку долговых обязательств или банковских акций, свободно обращающихся на финансовой бирже.

Однако лучшим инвестиционным шагом будет вложение в расширение собственного бизнеса. Это подразумевает покупку долгосрочных финактивов (ОС или основных средств), использование которых в торговых или производственных процессах сформирует стабильные финансовые поступления.

Для определения успешности определённого инвестиционного проекта, бизнес-экспертами применяются конкретные методики анализа бизнес-планов. В оценке используются два ключевых механизма:

• IRR, иначе InternalRate of Return в переводе с английского — внутренняя норма доходности;
• NPV или Net PresentValue — чистая приведённая стоимость.

Расчёт NPV при помощи MS Exel

В MS Exel существует функция ЧПС, позволяющая осуществить расчёт чистой приведённой стоимости.

Функция ЧПС возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).

Синтаксис функции ЧПС:

ЧПС(ставка;значение1;значение2; ...)

гдеСтавка — ставка дисконтирования за один период.Значение1, значение2,… — от 1 до 29 аргументов, представляющих расходы и доходы.

Значение1, значение2, … должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.

ЧПС использует порядок аргументов значение1, значение2, … для определения порядка поступлений и платежей. Убедитесь в том, что ваши платежи и поступления введены в правильном порядке.

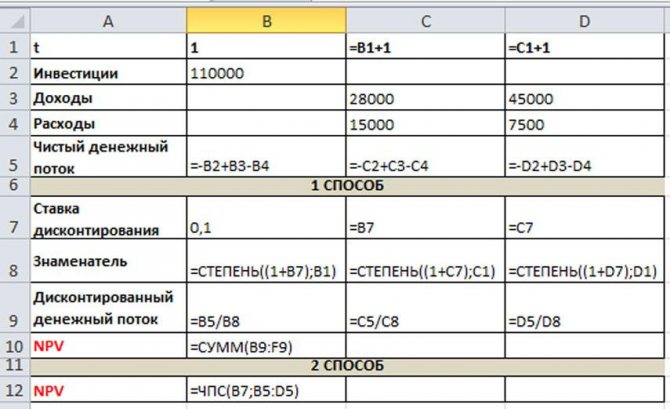
Рассмотрим пример расчёта NPV на базе 4-х альтернативных проектов.

В результате проведённых расчётов проект А следует отклонить, проект Б находится в точке безразличия для инвестора, а вот проекты В и Г следует использовать для вложения средств. При этом, если необходимо выбрать только один проект, то предпочтение следует отдать проекту В, невзирая на то, что сумму недисконтированных денежных потоков за 10 лет он генерирует меньше, чем проект Г.

Какую ставку использовать для дисконтирования

При расчете показателей эффективности проекта, и чистого дисконтированного дохода в том числе, инвестор рано или поздно сталкивается с проблемой выбора ставки дисконтирования.

Однозначно правильного ответа, какую ставку дисконтирования использовать, нет. Но есть рекомендации согласно здравому смыслу, ведь желаемая ставка – это норма прибыли для инвестора с учетом всех рисков проекта.

Допустим, у инвестора имеется три альтернативных способа вложить имеющиеся средства:

1. Открыть вклад в банке.
2. Инвестировать в акции «голубой фишки».
3. Инвестировать в ИТ-стартап.

Понятно, что риски нарастают от первого варианта к третьему, значит, здравый инвестор будет требовать более высокой доходности от третьего вложения, чем от второго и тем более от первого. Но насколько более высокой?

Есть несколько подходов к определению ставки дисконтирования:

1. Учет только показателя инфляции. Такой подход работает в основном для безрисковых и низкорисковых вложений и используется редко.
2. Интуитивный, основанный на опыте инвестора. Подход не научный, но используется часто, требует минимальных затрат времени, поэтому имеет право на существование.
3. Приравнивание ставки дисконтирования к стоимости капитала инвестора (WACC). Средневзвешенный капитал инвестора состоит из уже имеющихся проектов (бизнесов) и приносит какую-то доходность. Использование WACC означает, что инвестор сравнивает доходность от рассматриваемого проекта с доходностью уже проведенных инвестиций.
4. Расчет ставки дисконтирования на основании прошлых периодов с использованием прогнозирования по линиям трендов. Работает, только если есть накопленная статистика по похожим проектам. Фактически для расчета берется динамика ставки дисконта на рынках схожих инвестиций минимум за три года и формируется обоснованный прогноз.
5. Для уникальных инвестиций, по которым нет еще накопленного опыта и высоки риски, используется метод расчета с учетом рисков. На практике этот метод используется наиболее часто, так как у редкого инвестора есть статистические данные по аналогичным вложениям. Поэтому остановимся на нем подробнее.

Формула расчета ставки дисконтирования с учетом рисков:

Где i – барьерная ставка

iб – безрисковая ставка, минимальная прибыль, которую хочет получить инвестор в условиях отсутствия рисков

N – количество рисков

n– порядковый номер риска

Rn – премия за n-ный номер риска

Перед проведением расчета необходимо перечислить и взвесить все риски проекта: производственные, финансовые, коммерческие, политические, технологические и прочие. «Взвесить» означает присвоить каждому риску коэффициент. Критическим рискам присваивается самый высокий коэффициент, серьезным – ниже ит.д. Сумма коэффициентов по всем рискам должна быть равна единице.

В результате проведения расчета вы получите обоснованную ставку, по которой будете производить дисконтирование денежных потоков проекта.

Пример расчёта NPV

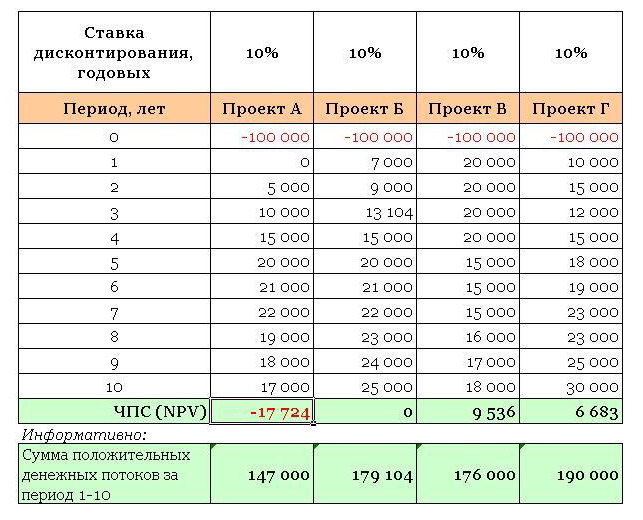
Пример расчета для трёх условных проектов позволяет, как рассчитать NPV, так и определить, какой из проектов будет более привлекательным для инвестирования.

Согласно условиям примера:

• начальные инвестиции – ICo – в каждый из трёх проектов равны 400 у.е.,
• норма прибыли – ставка дисконтирования – составляет 13%,
• прибыль, которые могут приносить проекты (по годам), расписана в таблице на 5-летний срок.

Рассчитаем чистый дисконтированный доход, чтобы выбрать наиболее выгодный для инвестирования проект. Фактор дисконтирования 1/(1 + R)t для интервала в один год будет t = 1: 1/(1+0,13)1 = 0,885. Если пересчитать NPV каждого сценария по годам с подстановкой в формулу определяющих значений, то получается, что для первого проекта NPV= 0,39, для второго – 10,41, для третьего – 7,18.

Однако сравниваемые проекты могут иметь разную продолжительность (жизненный цикл). Поэтому нередки ситуации, когда, например, при сравнении трёхлетнего и пятилетнего проектов NPV будет больше у пятилетнего, а среднее значение по годам – у трёхлетнего. Чтобы не возникло противоречий, рассчитываться в таких ситуациях должна ещё и среднегодовая норам доходности (IRR).

Кроме того, объём первоначальных инвестиций и ожидаемая прибыль известны не всегда, что создаёт сложности в применении расчётов.

Определение ставки дисконтирования (r) для инвестиционного проекта

Расчет ставки дисконтирования является важной задачей в расчете текущей стоимости инвестиционного проекта. Ставка дисконтирования представляет собой альтернативную доходность, которую мог бы получить инвестор

Одна из самых распространенных целей определения ставки дисконтирования – оценка стоимости компании.

Для оценки ставки дисконтирования используют такие методы как: модель CAPM, WACC, модель Гордона, модель Ольсона, модель рыночных мультипликаторов Е/Р, рентабельность капитала, модель Фамы и Френча, модель Росса (АРТ), экспертная оценка и т.д. Существует множество методов и их модификаций для оценки ставки дисконта. Рассмотрим в таблице преимущества и исходные данные, которые используются для расчета.

Методы	Преимущества	Исходные данные для расчета
Модель CAPM	Учет влияния рыночного риска на ставку дисконтирования	Котировки обыкновенных акций (биржа ММВБ)
Модель WACC	Возможность учесть эффективность использования как собственного, так и заемного капитала	Котировки обыкновенных акций (биржа ММВБ), процентные ставки по заемному капиталу
Модель Гордона	Учет дивидендной доходности	Котировки обыкновенных акций, дивидендные выплаты (биржа ММВБ)
Модель Росса	Учет отраслевых, макро и микро факторов, определяющих ставку дисконтирования	Статистика по макроиндикаторам  (Росстат)
Модель Фамы и Френча	Учет влияния на ставку дисконтирования рыночных рисков, размера компании и ее отраслевой специфики	Котировки обыкновенных акций (биржа ММВБ)
На основе рыночных мультипликаторов	Учет всех рыночных рисков	Котировки обыкновенных акций (биржа ММВБ)
На основе рентабельности капитала	Учет эффективность использования собственного капитала	Бухгалтерский баланс
На основе оценки экспертов	Возможность оценки венчурных проектов и различных трудно формализуемых факторов	Экспертные оценки, рейтинговые и бальные шкалы

Изменение ставки дисконтирования нелинейно влияет на изменение величины чистого дисконтированного дохода, данная зависимость показана на рисунке ниже. Поэтому необходимо при выборе инвестиционного проекта не только сравнивать значения NPV, но и характер изменения NPV при различных значениях ставки. Анализ различных сценариев позволяет выбрать менее рискованный проект.

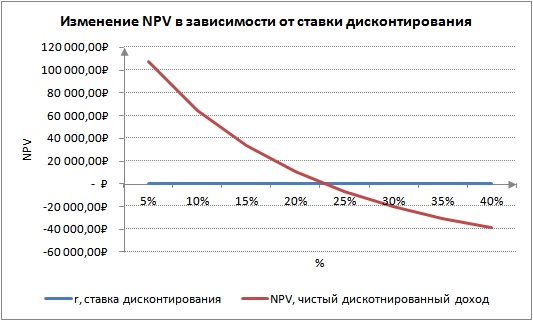
Про ставку дисконтирования и современные методы и формулы ее расчета, вы можете более подробно прочитать в моей статье: Ставка дисконтирования. 10 современных методов расчета.

Алгоритм и формула расчета ЧДД

ЧДД рассчитывается с использованием такой формулы:

где обозначения имеют следующий смысл:

Расчет денежных потоков

• CF – сальдо потока денежного, рассчитанного как разница между тем, что предприятие получило, и тем, что потратило
• t – количество лет, за который производится расчет
• r – ставка дисконтирования инвестиции
• n – продолжительность внедрения самого инвестиционного проекта

При изучении денежных потоков и их приведенной стоимости очень важно подойти непосредственно к выбору ставки дисконтирования. При осуществлении ее выбора необходимо учитывать не только особенности теории стоимости денег во времени, но и учитывать в обязательном порядке риск неопределенности

Лучше в качестве ставки дисконтирования выбирать именно средневзвешенную стоимость капитала, вложенного в инвестиционный проект. По итогу такого выбора существует закономерность: чем будут больше риски неопределенности, тем больше будет сама ставка, и наоборот.

ЧДД проектов: какой выбрать

Есть два инвестиционных проекта с инвестиционными вложениями в 10 тыс. рублей. Известны денежные потоки по каждому проекту по годам. Проект А: 5, 4, 3, 1. Проект Б имеет такие денежные потоки: 1, 3, 4, 6. Ставка дисконтирования 10%. Какой проект лучше?

Для начала необходимо рассчитать ЧДД для проекта А за каждый год:

• 5 / (1 + 0,1) в 1-й степени = 4545,5
• 4 / (1 + 0,1) во 2-й степени = 3305,8
• 3 / (1 + 0,1) в 3-й степени = 2253,9
• 1 / (1 + 0,1) в 4-й степени = 683,0

По результатам расчета ЧДД потока по проекту инвестирования А за 4-е года составит: 10788,2 (все ЧДД за четыре года суммируются: 4545,5 +…+ 683). Если отнять первоначальные капиталовложения, то ЧДД = 10788,2 – 10000 = 788,2.

По аналогии рассчитывается ЧДД по проекту Б, где она составит 491,5.

Вывод: вкладывать деньги можно в оба проекта, но выгоднее в проект А.

Формула расчёта NPV

Для расчёта NPV необходимо:

1. Составить прогнозный график денежных потоков по инвестиционному проекту в разрезе периодов. Денежные потоки должны включать как доходы (притоки средств), так и расходы (осуществляемые инвестиции и прочие затраты по реализации проекта).
2. Определить размер ставки дисконтирования. По сути, ставка дисконтирования отражает предельную норму стоимости капитала инвестора. Например, если для инвестирования будут использованы заёмные средства банка, то ставкой дисконтирования будет являться эффективная ставка процента по кредиту. Если же будут использованы собственные средства инвестора, то за ставку дисконтирования может быть взята ставка процента по банковскому депозиту, ставка доходности по государственным облигациям и т.п.

Расчёт NPV осуществляется по следующей формуле:

гдеNPV (Net Present Value) — чистая текущая стоимость инвестиционного проекта;CF (Cash Flow) — денежный поток;r — ставка дисконтирования;n — общее количество периодов (интервалов, шагов) i = 0, 1, 2, …, n за весь срок инвестирования.

В данной формуле CF соответствует объёму первоначальных инвестиций IC (Invested Capital), т.е. CF= IC. При этом денежный поток CF имеет отрицательное значение.

Поэтому, вышеуказанную формулу можно модифицировать:

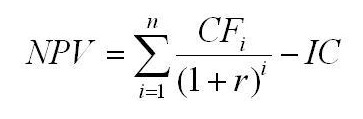
Если инвестиции в проект осуществляются не одномоментно, а на протяжении ряда периодов, то инвестиционные вложения также должны быть продисконтированны. В таком случае формула NPV проекта примет следующий вид: