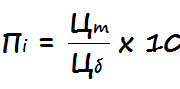Факторный анализ

ФАКТОРНЫЙ АНАЛИЗ: ОБЩАЯ ХАРАКТЕРИСТИКА И СПОСОБЫ ПРОВЕДЕНИЯ

Факторный анализ — это способ комплексного и системного исследования влияния отдельных факторов на размер итоговых показателей. Основная цель проведения такого анализа — найти способы увеличить доходность фирмы.

Факторный анализ позволяет определить общее изменение прибыли в текущем периоде по отношению к предыдущему (базовому) периоду или изменение фактических показателей прибыли по отношению к плану, а также влияние на эти изменения следующих факторов:

• объем продажи продукции;
• себестоимость реализуемой продукции;
• цены реализации;
• ассортимент реализуемой продукции.

Таким образом, с помощью факторного анализа можно установить объем продаж, себестоимость или цену реализации, которые увеличат прибыль компании, а факторный анализ по ассортименту реализуемой продукции даст возможность выявить товар, который продается лучше всего, и товар, пользующийся наименьшим спросом.

Показатели для факторного анализа берут из бухгалтерского учета. Если анализируют итоги за год, то используют данные формы № 2 «Отчет о финансовых результатах».

Факторный анализ можно проводить:

1) способом абсолютных разниц;

2) способом цепных подстановок.

Математическая формула модели факторного анализа прибыли от продаж:

ПР = V_прод × (Ц – S_ед),

где ПР — прибыль от продаж (плановая или базовая);

V_прод — объем продаж продукции (товаров) в натуральных величинах (штуки, тонны, метры и т. д.);

Ц — продажная цена единицы реализованной продукции;

S_ед — себестоимость единицы реализованной продукции.

Способ абсолютных разниц

За основу факторного анализа берется математическая формула ПР (прибыль от продаж). Формула включает три анализируемых фактора:

• объем продаж в натуральных единицах;
• цену;
• себестоимость одной единицы продаж.

Рассмотрим ситуации, влияющие на прибыль. Определим изменение величины прибыли за счет каждого фактора. Расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей. Приведем формулы расчета для каждой ситуации, оказавшей влияние на прибыль.

Ситуация 1. Влияние на прибыль объема продаж:

ΔПР_объем = ΔV_прод × (Ц_план – S_{ед. план}) = (V_{прод. факт} – V_{прод. план}) × (Ц_план – S_{ед. план}).

Ситуация 2. Влияние на прибыль продажной цены:

ΔПР_цена = V_{прод. факт} × ΔЦ = V_{прод. факт} × (Ц_факт – Ц_план).

Ситуация 3. Влияние на прибыль себестоимости единицы продукции:

ΔПР_Sед = V_{прод. факт} × (–ΔS_ед) = V_{прод. факт} × (–(S_{ед. факт} – S_{ед. план})).

Способ цепной подстановки

Используя такой метод, сначала рассматривают влияние одного фактора при неизменности прочих, затем второго и т. д. За основу берут все ту же математическую формулу модели факторного анализа прибыли от продаж.

Выявим влияние факторов на сумму прибыли.

Ситуация 1. Изменение объема продаж.

ПР1 = V_{прод. факт} × (Ц_план – S_{ед. план});

ΔПР_объем = ПР1 – ПР_план.

Ситуация 2. Изменение цены продаж.

ПР2 = V_{прод. факт} × (Ц_факт – S_{ед. план});

ΔПР_цена = ПР2 – ПР1.

Ситуация 3. Изменение себестоимости продаж единицы продукции.

ПР_Sед = V_{прод. факт} × (Ц_факт – S_{ед. факт});

ΔПР_Sед = ПР3 – ПР2.

Условные обозначения, применяемые в приведенных формулах:

ПР_план — прибыль от реализации (плановая или базовая);

ПР1 — прибыль, полученная под влиянием фактора изменения объема продаж (ситуация 1);

ПР2 — прибыль, полученная под влиянием фактора изменения цены (ситуация 2);

ПР3 — прибыль, полученная под влиянием фактора изменения себестоимости продаж единицы продукции (ситуация 3);

ΔПР_объем — сумма отклонения прибыли при изменении объема продаж;

ΔПР_цена — сумма отклонения прибыли при изменении цены;

ΔП_Sед — сумма отклонения прибыли при изменении себестоимости единицы реализованной продукции;

ΔV_прод — разница между фактическим и плановым (базисным) объемом продаж;

ΔЦ — разница между фактической и плановой (базисной) ценой продаж;

ΔS_ед — разница между фактической и плановой (базисной) себестоимостью единицы реализованной продукции;

V_{прод. факт} — объем продаж фактический;

V_{прод. план} — объем продаж плановый;

Ц_план — цена плановая;

Ц_факт — цена фактическая;

S_{ед. план} — себестоимость единицы реализованной продукции плановая;

S_{ед. факт} — себестоимость единицы реализованной продукции фактическая.

Замечания

1. Способ цепной подстановки дает те же результаты, что и способ абсолютных разниц.
2. Суммарное отклонение прибыли будет равно сумме отклонений под влиянием всех факторов, по которым проводят факторный анализ.

Понятие, задачи и типы факторного анализа

Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи. Одни из них непосредственно связаны между собой, другие  — косвенно. Каждое явление можно рассматривать как причину и как следствие.

Под факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Различают следующие типы факторного анализа: детерминированный и стохастический; прямой и обратный; одноступенчатый и многоступенчатый; статический и динамический; ретроспективный (исторический) и перспективный (прогнозный) .

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. когда результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов.

Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при стохастической связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель.

При прямом факторном анализе исследование ведется дедуктивным способом — от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных связей способом логичной индукции — от частных, отдельных факторов к обобщающим. Факторный анализ может быть одноступенчатым и многоступенчатым. Первый тип используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. При многоступенчатом факторном анализе проводится детализация факторов a и b на составные элементы с целью изучения их поведения. Детализация факторов может быть продолжена и дальше.

Необходимо различать также статический и динамический факторный анализ. Первый вид применяется при изучении влияния факторов на результативные показатели на соответствующую дату. Другой вид представляет собой методику исследования причинно-следственных связей в динамике.

Факторный анализ может быть ретроспективным, который изучает причины изменения результативных показателей за прошлые периоды, и перспективным, который исследует поведение факторов и результативных показателей в перспективе.

1. Отбор факторов для анализа исследуемых результативных показателей.

2. Классификация и систематизация факторов с целью обеспечения комплексного и системного подхода к исследованию их влияния на результаты хозяйственной деятельности.

3. Определение формы зависимости и моделирование взаимосвязей между факторными и результативными показателями.

4. Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.

5. Работа с факторной моделью (практическое ее использование для управления экономическими процессами) .

Отбор факторов для анализа того или другого показателя осуществляется на основе теоретических и практических знаний, приобретенных в этой отрасли. При этом обычно исходят из принципа: чем больший комплекс факторов исследуется, тем точнее будут результаты анализа.

Самый главный методологический аспект в АХД — расчет влияния факторов на величину результативных показателей, для чего в анализе используется целый арсенал способов, сущность, назначение, сфера применения которых и процедура расчетов рассматриваются в следующих главах. И наконец, последний этап факторного анализа — практическое использование факторной модели для подсчета резервов прироста результативного показателя, для планирования и прогнозирования его величины при изменении производственной ситуации.

Литература:

1. Савицкая, Г. В. Анализ хозяйственной деятельности предприятий АПК: Учеб. пособие. — 4-е изд., испр. и доп. —  Мн.: Новое знание, 2004. — 736 с.

2. Савицкая, Г. В. Анализ хозяйственной деятельности предприятий АПК: Учеб. пособие. — 6-е изд., стер. – Мн.: Новое знание, 2006. — 652 с.

Мастер настройки

• Критерий значимости факторов:
  • По собственному значению — отбираются только факторы с собственными значениями равными или большими 1. Считается, что те факторы, у которых этот показатель меньше 1, не вносят значительного вклада в объяснение результата.
  • По дисперсии — факторы отбираются по доле объясняемой дисперсии. В этом случае выбирают столько факторов, чтобы в сумме они объясняли не менее 70-75% дисперсии. В отдельных вариантах порог дисперсии может достигать 85-90%.
  • Задать число факторов — количество значимых факторов выбирается аналитиком самостоятельно.

Значение каждого критерия можно задать в специальном поле справа от соответствующей ему радиокнопки.

• Метод получения окончательного решения
  • Без вращения — исходные факторы, полученные методом главных компонент, остаются без изменений.
  • Варимакс — критерием является упрощение описания каждого фактора. В результате максимизируется нагрузка на каждый фактор относительно небольшого числа переменных, а факторные нагрузки остальных переменных минимизируются. Рекомендуется выбирать, когда требуется обеспечить высокую интерпретируемость результатов факторного анализа.
  • Квартимакс — данный критерий упрощает описание каждой переменной, то есть уменьшает число факторов, связанных с этой переменной.
• Ограничить число выходных факторов — необязательный флаг, при активации которого можно задать ограничивающее число выходных факторов в соответствующем поле области.

Понятие и назначение факторного анализа

При оценке деятельности организации за отчетный период руководство или предпринимателя в первую очередь интересует прибыль. Этот показатель, в свою очередь, зависит сразу от нескольких факторов. Его можно проследить с учетом:

• товарооборота;
• количества позиций товаров (ассортимента);
• издержек, связанных с покупкой товаров;
• себестоимостью и отпускной ценой;
• потоком клиентов и т.п.

Таким образом, факторный анализ позволяет понять, какие именно факторы влияют на исследуемый параметр, и в какой степени (т.е. установить конкретные количественные взаимосвязи). Также благодаря факторному анализу можно отследить и внутренние связи между факторами. При наличии устойчивых закономерностей можно установить корреляцию, например, между потоком клиентов и ассортиментом компании. Очевидно, что предприятие с большим количеством клиентов может потенциально может предоставить более широкую линейку товаров, а малая компания – более узкую.

Недостаток метода цепных подстановок

Минусов у этого метода не так уж и много, но при расчетах они имеют немаловажное значение. Во-первых, конечный результат (это величина влияния на совокупный показатель) напрямую зависит от последовательности подстановок

Если порядок замены значений поменять, то изменится и результат (величина влияния), причем каждого фактора. Во-вторых, если в расчетах опущен какой-то фактор, есть арифметическая ошибка, величина влияния некоторых факторов будет неточной.  При этом общий итог может быть верным.

Учитывая это, следует придерживаться следующей последовательности в расчетах:

1. Установить взаимосвязь всех имеющихся факторов.
2. Разделить их на количественные и качественные.
3. Выяснить, как, в каком порядке нужно их подменять.

Это главный недостаток метода, который надо учитывать при калькуляциях. Устранить его можно при помощи математических способов анализа, но лучше, конечно, до этого не доводить. 

Способ цепных подстановок. Факторный анализ

Под факторным анализом понимают многомерность метода, который применяют для комплексного исследования, выяснения степени воздействия факторов на величину итоговых показателей. Когда связь между факторами и этими показателями имеет функциональный характер, влияние факторов изучают при помощи детерминированного факторного анализа. Вот тогда-то и применяются способ цепных подстановок. Хотя, помимо него, еще используют и другие способы, например:

• относительных или абсолютных разниц;
• индексный; 
• интегральный и др.

Первые два способа, а также цепная подстановка базируются на элиминировании, что подразумевает исключение, устранение влияния всех факторов на величину соответствующего показателя, помимо одного. Простыми словами, все факторы подлежат изменению не зависимо друг от друга. Сначала меняется только один, затем только два, потом только три. Но другие во время их изменений остаются неизменными. Это позволяет выяснить влияние каждого отдельно взятого фактора на рассматриваемый показатель. 

Среди применяемых способов детерминированного факторного анализа самыми часто используемыми являются именно цепные подстановки. Их универсальность позволяет, как уже было сказано выше, применять его в расчетах для всех факторных моделей. Тем не менее, у них есть существенный недостаток. Факторы не зависят друг от друга, влияют только на совокупный (анализируемый) показатель и при расчетах их нужно заменять в строгой порядке, иначе результаты будут неточными. 

Кстати сказать, устранить этот недостаток может интегральный способ детерминированного факторного анализа. Месторасположение факторов при калькуляции этим способом не сказывается на результате их влияния. Поэтому он выдает более точные значения при установлении степени воздействия факторов на показатель. 

Диаграммы в Excel для факторного анализа

На днях приезжала моя теща и попросила помочь ей с построением достаточно замороченных диаграмм в Excel’е (для презентации). Опыт оказался интересным и которым я, собственно, хочу поделиться.

Итак, имеем два значения – одно плановое, второе проектное (или базовое и отчетное) и имеем значения отклонения факторов. Задача: построить в Excel красивую диаграмму отображения этих факторов.

Рис.0. Окончательный результат.

Создаем в Excel таблицу, в которой у нас находятся необходимые данные (см.рис.1).

Рис.1. Исходные данные

После этого разносим их следующим образом (рис.2)

Рис.2. Подготовка данных

Теперь подпишем столбцы – столбец I – Значение, далее – Основа, далее Влияние фактора (рис.3).

Рис.3. Названия столбцов.

В качестве базовой диаграммы мы будем использовать либо гистограмму либо линейчатую с наполнением.

Рис.4. Используемые типы диаграмм

Теперь поясню на рис.5 что я имею в виду под основой – это такое значение некоторого ряда которое позволит построить нам диаграмму максимально точно.

В вычислении значений этого ряда поступаем следующим образом:

1. Значение первой основы (сразу после базового значения) принимаем равным либо базовому значению (если первый фактор имеет позитивное влияние) либо (базовое значение – величина влияния) – если фактор имеет негативное влияние.

2. Для последующих основ применяется та же схема. Если значение фактора положительное, то за основу берем результирующее значение, полученное на предыдущем факторе. Если же отрицательное, то берем (результирующее – абсолютное значение негативного фактора).

Что такое основа легко понять по рис.5.

Ту величину, которую я назвал “Влияние фактора” вычисляем как значение изменения фактора по модулю (абсолютное значение) с помощью функции ABS() – рис.6.

Рис.6. Вычисленные значения “Влияния фактора”

Далее по описанному выше алгоритму рассчитываем значения основы для каждого фактора.

Для первой основы используются следующая функция:

=ЕСЛИ(L6>0;I5;I5+L6) — т.е. если первый фактор больше нуля, то берем базовое значение, в противном случае берем базовое + значение изменения фактора (в нашем примере получается просто 100).

Для всех последующих:

=ЕСЛИ(L7>0;M6;M6+L7) — т.е. если фактор больше нуля, то берем полученное на предыдущем факторе результирующее значение, в противном случае берем базовое + значение изменения фактора.

Ахтунг! Не забывайте про правила сложения – если я говорю “плюс значение”, это значит, что подразумевается не абсолютное значение, а позитивное или негативное. Т.е. для третьего фактора получим следующую логику:

Значение изменения фактора меньше нуля, следовательно берем сумму предыдущего результирующего значения и значения изменения фактора, т.е. основа будет равна 170+(-30)=170-30=140.

Результирующее значение вычисляется по формуле:

=ЕСЛИ(L6>0;J6+L6;J6) – т.е. если изменения фактора позитивное, то результирующим значением будет сумма предыдущего результирующего значения и величины изменения фактора, а в противном случае – просто значение основы. Далее переходим уже непосредственно к построению диаграммы. Выделяем ячейки от названия категорий до столбца “Влияние фактора” включительно.

Рис.7. Выделяемая область.

И вставляем необходимый тип диаграммы (в данном случае – гистограмму).

Рис.8. Полученный результат

Дальше наводим красоту – переносим на новый лист диаграмму и заодно поправляем мою ошибку в выборе исходных данных (Отчетное значение принимаем 160, а не 150).

Удаляем вертикальную ось, удаляем основные вертикальные и горизонтальные линии осей и у нас получается нечто вроде рис.9.

Дальше в свойствах ряда изменяем боковой зазор до 10% и ряду “Основа” выставляем отсутствие заливки и линий – т.е. делаем его невидимым.

Понятие факторного анализа

Факторный анализ – это метод изучения взаимосвязей между переменными значениями.

Считается, что переменные, которые известны исследователю, находятся в зависимости от меньшего числа факторов и имеют меньшую тенденцию к проявлению ошибок. С помощью этого метода математического исследования можно решить две глобальных задачи:

1. Сформировать всестороннее описание объекта, а затем скомпоновать его.
2. Выявить скрытые факторы, которые влияют на линейную взаимосвязь изучаемых объектов и явлений.

Применение факторного анализа позволяет реализовать сразу несколько целей исследования. Прежде всего, он помогает установить взаимосвязи между переменными, а также сократить их число для описания зависимости. Для удобства схожие факторы группируют, что облегчает модель, а также делает ее более наглядной. При объединении факторов их влияние на объект будет выше, а значит, ярче проявятся свойства, связанные с его изменениями.

Группировка позволяет отследить скрытые факторы влияния

Это свойство особенно важно при исследовании социально-экономических явлений. Именно скрытые переменные, проявляющиеся в изменении объектов, называются факторами. Попробуй обратиться за помощью к преподавателям

Попробуй обратиться за помощью к преподавателям

Чтобы определить наиболее значимые факторы применяются метод главных компонент. Его сущность заключается в замене взаимосвязанных величин не связанными между собой факторами. Для упрощения интерпретации результатов из уравнения могут исключаться менее информативные данные. Метод главных компонент является единственным математически обоснованным методом факторного анализа.

Факторный анализ имеет несколько форм. Он может быть разведочным, то есть направленным на выявление скрытых факторов. Конфирматорный анализ подтверждает гипотезы, относящиеся к исследованию числа факторов и оказываемых ими нагрузках.

Структурное моделирование уравнение

Программное обеспечение для моделирования структурных уравнений обычно используется для выполнения подтверждающего факторного анализа. LISREL , EQS, AMOS, Mplus и пакет lavaan в R — популярные программы. CFA также часто используется в качестве первого шага для оценки предлагаемой модели измерения в модели структурного уравнения. Многие правила интерпретации, касающиеся оценки соответствия модели и модификации модели при моделировании структурными уравнениями, в равной степени применимы к CFA. CFA отличается от моделирования структурным уравнением тем, что в CFA нет направленных стрелок между скрытыми факторами . Другими словами, в то время как в CFA не предполагается, что факторы напрямую вызывают друг друга, SEM часто определяет конкретные факторы и переменные как причинные по своей природе. В контексте SEM CFA часто называют «моделью измерения», а отношения между скрытыми переменными (с направленными стрелками) называют «структурной моделью».

Факторный анализ

Определение

Факторный анализ  – это процедура, с помощью которой большое число переменных, сводится к меньшему количеству независимых влияющих величин, называемых факторами. При этом в один фактор объединяются переменные (признаки), сильно коррелирующие (связанные) между собой. Переменные (признаки), относящиеся к разным факторам слабо коррелируют между собой.

Области применения факторного анализа

Факторный анализ используется при исследовании сложных объектов и систем (например, в психологии, биологии, социологии, экономике и др.) в том случае, когда напрямую невозможно измерять величины, определяющие свойства этих объектов (так называемые факторы). Однако для измерения доступны другие величины (переменные, признаки), которые зависят от этих факторов. Иными словами, фактор, который мы не можем измерить напрямую, проявляется в изменении нескольких переменных.

В области физической культуры и спорта в роли переменных могут выступать результаты тестирования уровня технической, физической, тактической подготовленности спортсменов, а также результаты медико-биологических и педагогических исследований.

Виды факторного анализа

Существует два основных вида факторного анализа – эксплораторный (исследовательский, разведочный) и конфирматорный (подтверждающий гипотезу).

Более подробно о методах статистической обработки данных рассказано в книгах:

• «Факторный анализ в педагогических исследованиях в области физической культуры и спорта»
• «Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта»
• «Компьютерная обработка данных экспериментальных исследований»

Эксплоаторный факторный анализ

Эксплораторный факторный анализ проводится на ранних этапах исследования, когда почти ничего не известно о структуре изучаемого явления и имеется значительное количество исходных данных. Цель проведения такого анализа – выявление латентной внутренней структуры и снижение размерности, то есть сокращение количества исследуемых переменных за счет объяснения их через новые факторные переменные. В ходе этого анализа, если необходимо, формулируются гипотезы, которые могут быть использованы для дальнейшего исследования.

Конфирматорный факторный анализ

Конфирматорный факторный анализ проводится для подтверждения уже выработанных гипотез. Этот вид факторного анализа  имеет строгие показатели и строгие критерии. Он предполагает, что уже выявлено какое-то количество факторов, необходимых для исследования и служит инструментом для проверки правильности выработанных гипотез, подтверждения выбранной структуры.  Изучаемые факторы тщательно продумываются и подбираются.

Исследователями в основном используется эксплораторный факторный анализ.

Бююль, А. SPSS: Искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей /А. Бююль, П. Цефель.– СПб: Диасофт.– СПб, 2001.– 608 с.
Дубров, А.М. Многомерные статистические методы для экономистов и инженеров /А.М. Дубров, В.С. Мхитарян, Л.И. Трошин /Учебн. для студ. эконом. специальностей ВУЗов.– М.: Финансы и статистика, 2000.
Дюк, В. Обработка данных на ПК в примерах / В. Дюк.– СПб: Питер, 1997. – 240 с.
Зациорский, В.М. Кибернетика, математика, спорт / В.М. Зациорский.– М.: Физкультура и спорт, 1969.–197 с.
Зациорский В

Осторожно: статистика! / В. Зациорский //Теория и практика физической культуры, 1989.– № 2.–С

52-55.
Ким, Дж.-О. Факторный анализ: статистические методы и практические вопросы / Дж.- О. Ким, Ч.У. Мьюллер // Факторный, дискриминантный и кластерный анализ / Пер.с англ. – М.: Финансы и статистика, 1989.– С. 5–74.
Масальгин, Н.А. Многомерный статистический анализ в исследованиях по физиологии спорта // Метод. разработка для аспирантов, преподавателей и слушателей Высшей школы тренеров и факультета усовершенствования / Н.А. Масальгин, А.С. Медведев.– М., 1991.– 35 с.
Самсонова, А.В. Факторный анализ. Направления применения и неиспользованные возможности /А.В. Самсонова //Вестник Балтийской Педагогической Академии.- 2005.- вып. 62.- С. 67-75
Самсонова, А.В. Факторный анализ в педагогических исследованиях в области физической культуры и спорта: учеб. пособие / А.В. Самсонова, И.Э. Барникова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт-Петербург.– СПб.: , 2013. — 90 с.

фон

история

Факторный анализ был разработан психологом Чарльзом Спирменом для оценки тестов интеллекта . В 1904 году он показал, что результаты тестов можно в значительной степени объяснить одномерной личностной чертой , общим фактором ( g-фактором ). Обобщение многофакторного анализа приписывается Дж. К. Максвеллу Гарнетту (Steiger, 1979); его популяризировал в 1940-х годах Луи Леон Терстон .

Методы оценки максимального правдоподобия были предложены Лоули и Виктором Барнеттом в 1930-х и 1940-х годах; стабильный алгоритм был разработан в 1960-х Герхардом Дерфлингером и Карлом Густавом Йорескогом .

Однако по сей день, несмотря на плохие свойства сходимости, итерационный вариант анализа главных компонент также используется для извлечения факторов. Распространены неточности вплоть до полного уравнения факторного анализа и анализа главных компонент.

Приложения

Факторный анализ — это универсальный инструмент для вывода ненаблюдаемых причин, лежащих в основе этих явлений. Например, такие конструкции , как «интеллект» или «амбиции», нельзя измерить, но они рассматриваются как причина многих форм поведения. Однако, чтобы не выдавать ошибочные результаты, факторный анализ требует, по крайней мере, уровня интервальной шкалы для используемых данных . Данные социальных наук редко достигают такого уровня шкалы и в основном имеют номинальную или порядковую шкалу .

Иногда факторный анализ также используется для научных задач. Приведены примеры факторно-аналитической обработки звуковых сигналов (распознавание речи), при которых выделяются основные акустические факторы. Это упрощает понимание языковых наложений (объявления аэропортов, записи конференций) или наложенных музыкальных записей ( слепое разделение источников , анализ независимости (ICA), см. Также ).

По словам Маркуса Виртца и Кристофа Нахтигалля, факторный анализ обычно преследует три цели:

1. Уменьшение количества переменных : факторный анализ распознает группы переменных, в которых все переменные фиксируют схожую информацию. Если переменные суммированы внутри каждой однородной группы, результатом будет более экономичное представление общей информации.
2. Определение надежных измеряемых переменных : если переменные объединены в один фактор, этот фактор имеет более благоприятные метрологические свойства, чем отдельные переменные.
3. Аналитические цели : факторный анализ позволяет сделать вывод о скрытых переменных высшего уровня (например, интеллекта) из явных переменных (индикаторных переменных ).

Исследовательский факторный анализ служит исключительно для исследования скрытых структур образца или уменьшения размеров. Он не подходит для проверки существующих теорий. Подтверждающий факторный анализ является подходящей процедурой для этого .