Как округлить до десятых
Содержание:
Архив блога
-
►
2018
(2)
-
►
апреля
(1)
►
27 апр
(1)
-
►
февраля
(1)
►
08 фев
(1)
-
-
►
2017
(5)
-
►
декабря
(2)
►
13 дек
(2)
-
►
июля
(1)
►
14 июл
(1)
-
►
марта
(1)
►
22 мар
(1)
-
►
января
(1)
►
23 янв
(1)
-
-
►
2016
(7)
-
►
декабря
(1)
►
29 дек
(1)
-
►
октября
(2)
►
26 окт
(1)
►
13 окт
(1)
-
►
сентября
(1)
►
26 сен
(1)
-
►
марта
(1)
►
02 мар
(1)
-
►
февраля
(1)
►
19 фев
(1)
-
►
января
(1)
►
27 янв
(1)
-
-
►
2015
(11)
-
►
октября
(1)
►
23 окт
(1)
-
►
сентября
(1)
►
24 сен
(1)
-
►
июля
(3)
►
14 июл
(1)
►
13 июл
(1)
►
10 июл
(1)
-
►
апреля
(1)
►
23 апр
(1)
-
►
марта
(2)
►
27 мар
(1)
►
18 мар
(1)
-
►
февраля
(1)
►
04 фев
(1)
-
►
января
(2)
►
28 янв
(1)
►
22 янв
(1)
-
-
►
2014
(6)
-
►
декабря
(1)
►
18 дек
(1)
-
►
ноября
(1)
►
10 ноя
(1)
-
►
сентября
(1)
►
26 сен
(1)
-
►
июня
(1)
►
03 июн
(1)
-
►
мая
(1)
►
21 мая
(1)
-
►
февраля
(1)
►
18 фев
(1)
-
-
►
2013
(24)
-
►
декабря
(2)
►
17 дек
(1)
►
12 дек
(1)
-
►
ноября
(1)
►
08 ноя
(1)
-
►
октября
(5)
►
29 окт
(1)
►
28 окт
(1)
►
15 окт
(1)
►
04 окт
(2)
-
►
августа
(2)
►
13 авг
(1)
►
01 авг
(1)
-
►
июля
(1)
►
07 июл
(1)
-
►
июня
(6)
►
25 июн
(1)
►
21 июн
(1)
►
20 июн
(1)
►
19 июн
(1)
►
14 июн
(1)
►
11 июн
(1)
-
►
мая
(1)
►
06 мая
(1)
-
►
марта
(2)
►
31 мар
(1)
►
12 мар
(1)
-
►
февраля
(2)
►
18 фев
(1)
►
07 фев
(1)
-
►
января
(2)
►
23 янв
(1)
►
09 янв
(1)
-
-
►
2012
(34)
-
►
декабря
(2)
►
03 дек
(1)
►
01 дек
(1)
-
►
ноября
(7)
►
25 ноя
(1)
►
22 ноя
(2)
►
15 ноя
(1)
►
08 ноя
(1)
►
03 ноя
(1)
►
02 ноя
(1)
-
►
октября
(1)
►
18 окт
(1)
-
►
сентября
(4)
►
21 сен
(1)
►
10 сен
(3)
-
►
августа
(2)
►
25 авг
(1)
►
22 авг
(1)
-
►
июля
(2)
►
27 июл
(1)
►
03 июл
(1)
-
►
июня
(5)
►
12 июн
(2)
►
11 июн
(1)
►
08 июн
(1)
►
07 июн
(1)
-
►
мая
(10)
►
27 мая
(1)
►
24 мая
(2)
►
16 мая
(1)
►
14 мая
(2)
►
12 мая
(1)
►
11 мая
(1)
►
10 мая
(2)
-
►
января
(1)
►
30 янв
(1)
-
-
▼
2011
(19)
-
▼
ноября
(2)
►
30 ноя
(1)
-
▼
10 ноя
(1)
PHP, округление до десятков и сотен в большую сторону
-
-
►
сентября
(7)
►
23 сен
(1)
►
13 сен
(1)
►
12 сен
(2)
►
09 сен
(2)
►
01 сен
(1)
-
►
августа
(4)
►
30 авг
(1)
►
27 авг
(1)
►
26 авг
(1)
►
24 авг
(1)
-
►
июля
(1)
►
25 июл
(1)
-
►
июня
(1)
►
01 июн
(1)
-
►
апреля
(2)
►
27 апр
(1)
►
25 апр
(1)
-
►
марта
(2)
►
29 мар
(1)
►
19 мар
(1)
-
-
►
2010
(59)
-
►
декабря
(3)
►
24 дек
(1)
►
12 дек
(1)
►
11 дек
(1)
-
►
ноября
(5)
►
22 ноя
(2)
►
13 ноя
(2)
►
03 ноя
(1)
-
►
октября
(3)
►
12 окт
(1)
►
11 окт
(1)
►
01 окт
(1)
-
►
сентября
(3)
►
16 сен
(1)
►
15 сен
(2)
-
►
августа
(3)
►
28 авг
(1)
►
17 авг
(1)
►
02 авг
(1)
-
►
июля
(4)
►
14 июл
(1)
►
13 июл
(1)
►
01 июл
(2)
-
►
июня
(5)
►
29 июн
(1)
►
23 июн
(1)
►
21 июн
(1)
►
17 июн
(1)
►
11 июн
(1)
-
►
мая
(4)
►
26 мая
(1)
►
15 мая
(1)
►
13 мая
(1)
►
12 мая
(1)
-
►
апреля
(9)
►
26 апр
(1)
►
23 апр
(1)
►
15 апр
(3)
►
08 апр
(1)
►
07 апр
(2)
►
01 апр
(1)
-
►
марта
(5)
►
30 мар
(1)
►
15 мар
(1)
►
09 мар
(1)
►
08 мар
(1)
►
05 мар
(1)
-
►
февраля
(3)
►
22 фев
(1)
►
18 фев
(1)
►
17 фев
(1)
-
►
января
(12)
►
27 янв
(2)
►
24 янв
(1)
►
18 янв
(1)
►
14 янв
(1)
►
06 янв
(1)
►
05 янв
(1)
►
04 янв
(2)
►
02 янв
(3)
-
-
►
2009
(8)
-
►
декабря
(3)
►
24 дек
(1)
►
18 дек
(1)
►
09 дек
(1)
-
►
ноября
(1)
►
01 ноя
(1)
-
►
октября
(1)
►
12 окт
(1)
-
►
июля
(1)
►
29 июл
(1)
-
►
июня
(1)
►
19 июн
(1)
-
►
апреля
(1)
►
29 апр
(1)
-
-
►
2008
(6)
-
►
апреля
(1)
►
26 апр
(1)
-
►
марта
(1)
►
16 мар
(1)
-
►
февраля
(2)
►
27 фев
(1)
►
23 фев
(1)
-
►
января
(2)
►
15 янв
(1)
►
13 янв
(1)
-
-
►
2007
(9)
-
►
декабря
(3)
►
18 дек
(1)
►
17 дек
(1)
►
05 дек
(1)
-
►
ноября
(2)
►
29 ноя
(1)
►
28 ноя
(1)
-
►
июля
(4)
►
27 июл
(1)
►
21 июл
(1)
►
20 июл
(1)
►
19 июл
(1)
-
Способы округления чисел
Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.
Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .
math.ceil() — округление чисел в большую сторону
Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.
Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.
Пример:
math.ceil(5.15) # = 6 math.ceil(6.666) # = 7 math.ceil(5) # = 5
Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.
math.floor() — округление чисел в меньшую сторону
Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.
Пример:
math.floor(7.9) # = 7 math.floor(9.999) # = 9 math.floor(-6.1) # = -7
math.trunc() — отбрасывание дробной части
Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.
Примеры:
math.trunc(5.51) # = 5 math.trunc(-6.99) # = -6
Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .
Примеры:
int(5.51) # = 5 int(-6.99) # = -6
Нормальное округление
Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.
И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().
Примеры:
math.floor(9.999) # = 9 int(9.999) # = 9 math.ceil(-9.999) # = -9 int(-9.999) # = -9
Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.
Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:
def int_r(num):
num = int(num + (0.5 if num > 0 else -0.5))
return num
Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).
Примеры:
int_r(11.5) # = 12 int_r(11.4) # = 11 int_r(-0.991) # = -1 int_r(1.391) # = 1
round() — округление чисел
round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.
В Python 2
Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.
Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».
Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.
В Python 3
В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.
Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.
Примеры:
round(3.5) # = 4 round(9.5) # = 10 round(6.5) # = 6 round(-6.5) # = -6 round(-7.5) # = -8
Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.
Округление до сотых
У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.
Пример округления до нужного знака:
round(3.555, 2) # = 3.56 round(9.515,1) # = 9.5 round(6.657,2) # = 6.66
Правила округления десятичной дроби
Десятичную дробь можно округлить:
- до целого числа с точностью до единиц, десятков, сотен и т.д.;
- до определенного разряда дробной части: десятых, сотых, тысячных, десятитысячных и т.д.
Но, прежде чем перейти к правилам округления, давайте еще раз вспомним, из чего состоит десятичная дробь. В качестве примера – от тысяч до десятитысячных:
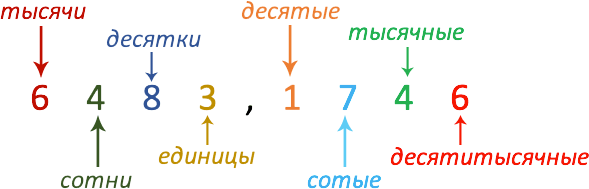
Округление дробной части
Итак, чтобы выполнить округление десятичной дроби, придерживаемся следующего плана действий:
- Отмечаем разряд, до которого следует округлить дробь. Его можно отделить от следом идущих цифр разделительной линией.
- Далее возможно два варианта (согласно правилам округления чисел):
- если после выбранного разряда идут цифры , 1, 2, 3 или 4, то цифру этого разряда мы оставляем той же, а все остальные цифры после линии убираем.
- если после выбранного разряда стоят цифры 5, 6, 7, 8 или 9, то к цифре этого разряда прибавляем единицу и, как в пункте выше, все цифры с правой стороны от линии убираем.
Пример 1: округлим 12,624 до десятых.
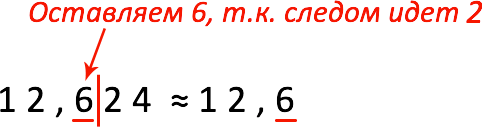
Пример 2: округлим 5,176 до сотых.

Если десятичную дробь требуется округлить до целого числа (до единиц), смотрим на цифру, которая идет сразу же после запятой (разряд – десятые). Если это 5, 6, 7, 8 или 9, то к единицам в целой части прибавляем число 1, а всю дробную часть отбрасываем. В остальных случаях просто убираем дробную часть без каких-либо изменений целой части.
Примеры округления десятичных дробей до целого числа:
- 2,15 ≈ 2;
- 4,64 ≈ 5;
- 7,063 ≈ 7;
- 12,814 ≈ 13.
Примечание: Если дробь требуется округлить до целого числа большего разряда, чем единицы (десятки, сотни, тысячи и т.д.), отбрасываем дробную часть, затем округляем полученный результат согласно правилам округления натуральных чисел.
Пример 1: выполним округление до десятков числа 156,71:
Пример 2: выполним округление до сотен числа 8134,145:
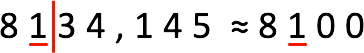
Особый случай: последняя цифра – ноль
Если в результате округления десятичной дроби последней цифрой в дробной части остается , его нельзя убирать. Это нужно для того, чтобы наглядно было понято, до какого разряда было выполнено округление.
Примеры округления с нулем на конце
- 5,01 ≈ 5,0 (до десятых);
- 3,199 ≈ 3,20 (до сотых).
Остановимся подробнее на втором примере. Т.к. в следующем разряде после сотых стоит цифра 9, значит по правилам округления к сотым мы прибавляем единицу: 9 + 1 = 10. Следовательно, в разряде сотых мы пишем ноль, а единицу прибавляем к десятым (1 + 1 = 2).
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Варианты округления 0,5 к ближайшему целому
Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:
- Математическое округление[источник не указан 189 дней] — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
- Округление до ближайшего чётного (в английском языке известно под названием англ. banker’s rounding — «округление банкира») — округление для этого случая происходит к ближайшему чётному числу, то есть 2,5 → 2; 3,5 → 4.
- Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике).
- Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.
Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.
Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.
Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.
Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.
- Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным рекуррентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
- Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.
Как работать с функциями в Excel
Мы рассмотрели самый простой способ убрать лишние знаки. Использовать его довольно удобно, если менять сами данные в таблице нам не нужно. Теперь мы переходим к использованию различных функций. Но сначала я хочу напомнить вам, что это такое, а также как с ними работать.
Функции ускоряют и упрощают вычисления. Например, нам надо посчитать сумму в столбце, в котором 100 значений. Мы можем делать это самым прямым способом “1+20+30+43…” и так 99 раз. Или написать встроенную команду “СУММ”, указать диапазон ячеек, и программа за секунду сделает расчеты.
Первый способ
Чтобы вручную написать формулу в ячейке с использованием функции, обязательно нужно:
- Поставить знак =.
- Правильно указать название.
- Открыть круглую скобку.
- Указать через точку с запятой аргументы, то есть данные, которые будут использоваться.
- Закрыть скобку.
Что может выступать аргументом математических формул:
- число,
- формула,
- диапазон ячеек.
Пример: функция “=СУММ(F21:F30)” посчитает сумму чисел, написанных в столбце F с позиции F21 до F30.
Эти правила нужно запомнить, иначе программа не сможет сделать вычисления, а будет выдавать ошибку такого вида.
Второй способ
Если неудобно писать команды вручную, то можно воспользоваться библиотекой, которая находится во вкладке “Формулы”.

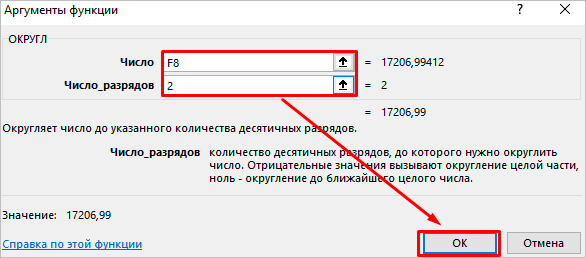
Нас в данный момент интересуют математические операции. Нажимаем на соответствующий раздел и выбираем нужную процедуру.
Откроется диалоговое окно, в котором легко понять, какие аргументы нужно указать. Заполните поля и нажмите “ОК”.
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды
Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых
Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной
Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Способы записи числа
Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:
Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.
В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:
Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.
Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):
Записать микросекунду в укороченном виде нам поможет .
Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .
Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:
Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.
Например:
Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:
Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).
Округление при работе с числами ограниченной точности
Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.
Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.
Округление рассчитанного значения погрешности
Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:
- 0,10; 0,12; 0,14; 0,16; 0,18;
- 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
- 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.
Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.
Пересчёт значений физических величин
Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.